
分析 (1)根据题意设增种m棵树,就可求出每棵树的产量,然后求出总产量W,再配方即可求解;
(2)根据题意,增种橙子树后产量为60000,解方程即可求出要保证增种橙子树后产量不降低,增种的数量范围.
解答 解:(1)设增种m棵树,果园橙子的总产量为W,W=(100+m)(600-5m)=-5(m-10)2+60500,
故当增种10棵橙子树,可以使果园橙子的总产量最多,最多为60500个;
(2)根据题意得-5(m-10)2+60500=60000,
解得:m1=0,m2=20,
所以要保证增种橙子树后产量不降低,增种的数量的范围为:0≤m≤20.
点评 此题主要考查了一元二次方程的应用和二次函数的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
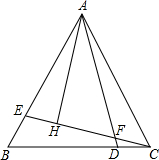 如图,△ABC是等边三角形,点D、E分别是BC边、AB边上的点,且BE=CD,连接AD、CE交于点F,过A作AH⊥CE于H,
如图,△ABC是等边三角形,点D、E分别是BC边、AB边上的点,且BE=CD,连接AD、CE交于点F,过A作AH⊥CE于H,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com