
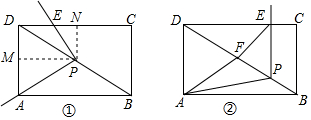
分析 (1)①根据两角相等证明相似;②根据上问的三角形相似得:$\frac{PM}{PN}=\frac{PA}{PE}$,根据根据矩形DMPN得:DM=PN,由直角△DMP的锐角正切可得结论;
(2)作辅助线,构建相似三角形,根据(1)中的结论得:tan∠ADB=$\frac{AP}{PE}=\frac{AB}{AD}$=$\frac{4}{3}$,证明△GAP∽△FPE,
则$\frac{AP}{PE}=\frac{AG}{PF}$,可求得PF的长,利用面积法求出AG的长,代入面积公式可得结论.
解答 证明:(1)如图①,
①∵∠EPA=90°,
∴∠APM+∠MPE=90°,
∵四边形ABCD是矩形,
∴∠ADC=90°,
∵PM⊥AD,PN⊥DC,
∴∠DMP=∠PND=90°,
∴四边形DMPN为矩形,
∴∠MPN=90°,
∴∠EPN+∠MPE=90°,
∴∠APM=∠EPN,
∵∠AMP=∠PNE=90°,
∴△PMA∽△PNE;
②∵△PMA∽△PNE,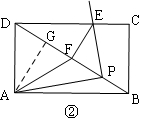
∴$\frac{PM}{PN}=\frac{PA}{PE}$,
∵四边形DMPN为矩形,
∴DM=PN,
在Rt△DPM中,tan∠ADB=$\frac{PM}{DM}$,
∴tan∠ADB=$\frac{PM}{PN}=\frac{PA}{PE}$;
(2)△PAF的面积不发生变化,理由是:
如图②,过A作AG⊥BD于G,
∵AD=BC=3,AB=4,∠DAB=90°,
∴BD=5,
∴S△ABD=$\frac{1}{2}$BD•AG=$\frac{1}{2}$AD•AB,
∴BD•AG=AD•AB,
∴AG=$\frac{3×5}{5}$=$\frac{12}{5}$,
∵∠APE=90°,
∴∠APG+∠GPE=90°,
∵∠AGP=90°,
∴∠APG+∠GAP=90°,
∴∠GPE=∠GAP,
∵∠AGP=∠EFP=90°,
∴△GAP∽△FPE,
∴$\frac{AP}{PE}=\frac{AG}{PF}$,
由(1)得:tan∠ADB=$\frac{AP}{PE}=\frac{AB}{AD}$=$\frac{4}{3}$,
∴$\frac{AG}{PF}$=$\frac{4}{3}$,
∴3AG=4PF,
∴PF=3×$\frac{12}{5}$×$\frac{1}{4}$=$\frac{9}{5}$,
∴S△APF=$\frac{1}{2}$PF•AG=$\frac{1}{2}$×$\frac{9}{5}$×$\frac{12}{5}$=$\frac{54}{25}$.
答:△PAF的面积是$\frac{54}{25}$.
点评 本题是相似三角形的综合题,难度适中,考查了相似三角形的性质和判定、矩形的性质及三角函数的定义,在证明两三角形相似时常利用两角对应相等证明相似,本题也是如此;在利用比例式求线段的长时,可以利用相似列比例式,也可以利用同角的三角函数列比例式.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
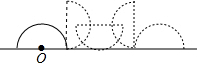 一个半圆形零件,直径紧贴地面,现需要将零件按如图所示方式,向前作无滑动翻转,使圆心O再次落在地面上止.已知半圆的半径为1m,则圆心O所经过的路线长是πm.(结果用π表示)
一个半圆形零件,直径紧贴地面,现需要将零件按如图所示方式,向前作无滑动翻转,使圆心O再次落在地面上止.已知半圆的半径为1m,则圆心O所经过的路线长是πm.(结果用π表示)查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 斜边与一条直角边对应成比例的两个直角三角形相似 | |
| B. | 两个等腰直角三角形相似 | |
| C. | 两边对应成比例且有一个角相等的两个三角形相似 | |
| D. | 各有一个角等于100°的两个等腰三角形相似 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 20 | B. | 24 | C. | 20或24 | D. | 24或26 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
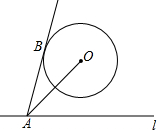 如图,点A是直线l上一点,AB切⊙O于点B,圆心O与点A间的最小距离是6cm,⊙O的半径为4cm,则AB的最小值是2$\sqrt{6}$.
如图,点A是直线l上一点,AB切⊙O于点B,圆心O与点A间的最小距离是6cm,⊙O的半径为4cm,则AB的最小值是2$\sqrt{6}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 第一天 | 第二天 | 第三天 | 第四天 | 第五天 | 第六天 | 第七天 | |
| 路程(km) | -8 | -11 | -14 | 0 | -16 | +41 | +8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com