
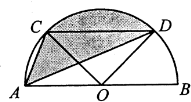
分析 由CD∥AB可知,点A、O到直线CD的距离相等,结合同底等高的三角形面积相等即可得出S△ACD=S△OCD,进而得出S阴影=S扇形COD,根据扇形的面积公式即可得出结论.
解答 解:∵弦CD∥AB,
∴S△ACD=S△OCD,
∴S阴影=S扇形COD=$\frac{∠COD}{360°}$•π•$(\frac{AB}{2})^{2}$=$\frac{90°}{360°}$×π×$(\frac{2}{2})^{2}$=$\frac{π}{4}$.
故答案为:$\frac{π}{4}$.
点评 本题考查了扇形面积的计算以及平行线的性质,解题的关键是找出S阴影=S扇形COD.本题属于基础题,难度不大,解决该题型题目时,通过分割图形找出面积之间的关系是关键.


科目:初中数学 来源: 题型:选择题
| A. | 3×107 | B. | 30×106 | C. | 0.3×107 | D. | 0.3×108 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
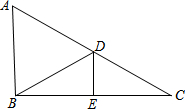 如图,△ABC中,D、E两点分别在AC、BC上,DE为BC的中垂线,BD为∠ADE的角平分线.若∠A=58°,则∠ABD的度数为何?( )
如图,△ABC中,D、E两点分别在AC、BC上,DE为BC的中垂线,BD为∠ADE的角平分线.若∠A=58°,则∠ABD的度数为何?( )| A. | 58 | B. | 59 | C. | 61 | D. | 62 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com