
 如图,等腰梯形ABCD中,AD∥BC,AD=$\sqrt{2}$,BC=4$\sqrt{2}$,∠B=45°,等腰直角三角板MEN的锐角顶点E在边BC上移动,一直角边始终经过点A,斜边与CD交于点F.若△ABE为等腰三角形,则CF的长等于$\frac{5}{2}$或4$\sqrt{2}$-3或2.
如图,等腰梯形ABCD中,AD∥BC,AD=$\sqrt{2}$,BC=4$\sqrt{2}$,∠B=45°,等腰直角三角板MEN的锐角顶点E在边BC上移动,一直角边始终经过点A,斜边与CD交于点F.若△ABE为等腰三角形,则CF的长等于$\frac{5}{2}$或4$\sqrt{2}$-3或2. 分析 过点A作AM⊥BC于M,过点D作DN⊥BC于N,根据等腰三角形的性质求出BM的长度,再求出AB,然后分①AE=BE时,△ABE、△CEF都是等腰直角三角形,求出BE的长,再求出CE的长,然后根据等腰直角三角形的性质求解即可;②AB=BE时,先求出CE的长度,再求出∠AEB的度数,再根据平角等于180°求出∠CEF,然后求出∠CFE,根据度数得到∠CEF=∠CFE,根据等角对等边的性质可得CF=CE;③AB=AE时,判断出△ABE、△CEF都是等腰直角三角形,然后根据等腰直角三角形的性质求解即可.
解答 解:如图,过点A作AM⊥BC于M,过点D作DN⊥BC于N,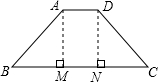
∵等腰梯形ABCD中,AD∥BC,BC=4AD=4$\sqrt{2}$,
∴BM=$\frac{1}{2}$(BC-AD)=$\frac{1}{2}$(4$\sqrt{2}$-$\sqrt{2}$)=$\frac{3\sqrt{2}}{2}$,∠C=∠B=45°,
∵∠B=45°,
∴AB=BM×$\sqrt{2}$=3,
①如图1,AE=BE时,∵∠B=45°,
∴∠BAE=∠B=45°,
∴△ABE是等腰直角三角形,
∴BE=$\frac{\sqrt{2}}{2}$AB=$\frac{3\sqrt{2}}{2}$
∴CE=BC-BE=4$\sqrt{2}$-$\frac{3\sqrt{2}}{2}$=$\frac{5\sqrt{2}}{2}$,
又∵∠CEF=180°-∠AEB-∠AEF=180°-90°-45°=45°,
∴△CEF是等腰直角三角形,
∴CF=$\frac{\sqrt{2}}{2}$CE=$\frac{5}{2}$;
②如图2,AB=BE时,∵∠B=45°,
∴∠AEB=$\frac{1}{2}$(180°-∠B)=$\frac{1}{2}$(180°-45°)=67.5°,
∴∠CEF=180°-∠AEB-∠AEF=180°-67.5°-45°=67.5°,
∴∠CFE=180°-∠C-∠CEF=180°-45°-67.5°=67.5°,
∴∠CEF=∠CFE,
∴CF=CE,
∵BC=4$\sqrt{2}$,AB=3,
∴CF=CE=BC-BE=4$\sqrt{2}$-3;
③如图3,AB=AE时,∠AEB=∠B=45°,
∴∠CEF=180°-∠AEB-∠AEF=180°-45°-45°=90°,
∴△ABE、△CEF都是等腰直角三角形,
∴BE=$\sqrt{2}$AB=3$\sqrt{2}$,
CE=BC-BE=4$\sqrt{2}$-3$\sqrt{2}$=$\sqrt{2}$,
∴CF=$\sqrt{2}$CE=$\sqrt{2}$×$\sqrt{2}$=2;
综上所述,CF的长为$\frac{5}{2}$或4$\sqrt{2}$-3或2.
故答案为:$\frac{5}{2}$或4$\sqrt{2}$-3或2.
点评 本题考查了等腰梯形的性质,等腰直角三角形的性质,熟记性质是解题的关键,难点在于根据腰长的不同,分情况讨论.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
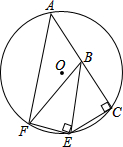 如图,AC为⊙O的弦,CE⊥AC交⊙O于E,B为AC上的一点,BC=CE,EF⊥BE交⊙O于F,⊙O的直径为13,BE=5$\sqrt{2}$.
如图,AC为⊙O的弦,CE⊥AC交⊙O于E,B为AC上的一点,BC=CE,EF⊥BE交⊙O于F,⊙O的直径为13,BE=5$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=(x-1)2-1 | B. | y=(x+1)2-1 | C. | y=(x+1)2+3 | D. | y=(x-1)2+3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com