
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 从
从![]() 点出发沿
点出发沿![]() 边向
边向![]() 以
以![]() 的速度移动,点
的速度移动,点![]() 从
从![]() 点出发沿
点出发沿![]() 向
向![]() 点以
点以![]() 的速度移动,当其中一个点到达终点时两个点同时停止运动,在两个点运动过程中,请回答:
的速度移动,当其中一个点到达终点时两个点同时停止运动,在两个点运动过程中,请回答:
![]() 经过多少时间,
经过多少时间,![]() 的面积是
的面积是![]() ?
?
![]() 请你利用配方法,求出经过多少时间,四边形
请你利用配方法,求出经过多少时间,四边形![]() 面积最小?并求出这个最小值.
面积最小?并求出这个最小值.
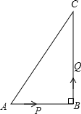
【答案】![]() 经过
经过![]() 秒,能使
秒,能使![]() 的面积等于
的面积等于![]() ;
;![]() 经过3秒时,四边形APQC面积最小,最小值为15.
经过3秒时,四边形APQC面积最小,最小值为15.
【解析】
(1)由题意,可设P、Q经过t秒,使△PBQ的面积为5cm2,则PB=6-t,BQ=2t,根据三角形面积的计算公式,S△PBQ=![]() BP×BQ,列出表达式,解答出即可;
BP×BQ,列出表达式,解答出即可;
(2)可设P、Q两点运动t秒时,四边形![]() 面积有最小值,则PB=6-t,BQ=2t,由S四边形APQC= S△ABC- S△PBQ可得关于t的函数,利用二次函数的性质即可求得答案.
面积有最小值,则PB=6-t,BQ=2t,由S四边形APQC= S△ABC- S△PBQ可得关于t的函数,利用二次函数的性质即可求得答案.
![]() 设P、Q经过t秒时,△PBQ的面积为5cm2,
设P、Q经过t秒时,△PBQ的面积为5cm2,
则PB=6-t,BQ=2t,
∵∠B=90°,AB=6cm,BC=8cm,![]() ,
,
![]() ,
,
![]() ,
,
解得![]() ,
,![]() (舍去),
(舍去),
所以![]() ,
,
故经过![]() 秒,能使
秒,能使![]() 的面积等于
的面积等于![]() ;
;
(2)设P、Q两点运动t秒时,四边形![]() 面积有最小值,则PB=6-t,BQ=2t,
面积有最小值,则PB=6-t,BQ=2t,
S四边形APQC= S△ABC- S△PBQ
=![]() -
-![]()
=(t-3)2+15,
∴当t=3时,![]() 的最小值为
的最小值为![]() ,
,
即经过3秒时,四边形![]() 面积最小,最小值为15.
面积最小,最小值为15.


科目:初中数学 来源: 题型:
【题目】如图,在边长为1的正方形网格中,两个三角形的顶点都在格点(网线的交点)上,下列方案中不能把△ABC平移至△DEF位置的是( )
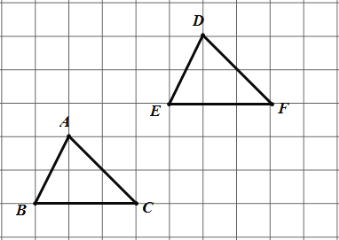
A.先把△ABC沿水平方向向右平移4个单位长度,再向上平移3个单位长度
B.先把△ABC向上平移3个单位长度,再沿水平方向向右平移4个单位长度
C.把△ABC沿BE方向移动5个单位长度
D.把△ABC沿BE方向移动6个单位长度
查看答案和解析>>
科目:初中数学 来源: 题型:
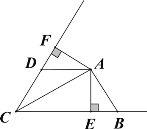
【题目】如图,AC平分∠BCD,AB=AD, AE⊥BC于E,AF⊥CD于F
(1)若∠ABE= 50° ,求∠CDA的度数.
(2)若AE=4,BE=2,CD=6,求四边形AECD 的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,以□ABCD的顶点A为圆心,AB为半径作圆,分别交AD,BC于点E、F,延长BA交⊙A于G.

(1)求证:![]() .
.
(2)若![]() 的度数为70°,求∠C的度数.
的度数为70°,求∠C的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先化简,再求值:(1)(2x+y)2+(x-y)(x+y)-5x(x-y),其中x=![]() +1,y=
+1,y=![]() -1.
-1.
(2)[(x+2y)2-(x+y)(3x-5y)-5y2]÷2x,其中x=-2,y=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某进口专营店销售一种“特产”,其成本价是20元/千克,根据以往的销售情况描出销量y(千克/天)与售价x(元/千克)的关系,如图所示.
(1)试求出y与x之间的一个函数关系式;
(2)利用(1)的结论:
①求每千克售价为多少元时,每天可以获得最大的销售利润.
②进口产品检验、运输等过程需耗时5天,该“特产”最长的保存期为一个月(30天),若售价不低于30元/千克,则一次进货最多只能多少千克?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①所示,某乘客乘高速列车从甲地经过乙地到丙地,假设列车匀速行驶.如图②表示列车离乙地路程y(千米)与列车从甲出发后行驶时间x(小时)之间的函数关系图像.
(1)甲、丙两地间的路程为千米;
(2)求高速列车离乙地的路程y与行驶时间x之间的函数关系式,并写出x的取值范围;
(3)当行驶时间x在什么范围时,高速列车离乙地的路程不超过100千米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD沿着直线BD折叠,使点C落在C/处,BC/交AD于E,AD=8,AB=4,DE的长=________________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com