
����Ŀ���ס������������ֱ��![]() ��
��![]() ���س�������ͬһ����·������У�������Է��ij����غ�����װж���5���Ӻ��ٰ�ԭ·��ԭ�ٶȷ��ظ��Եij����أ���֪
���س�������ͬһ����·������У�������Է��ij����غ�����װж���5���Ӻ��ٰ�ԭ·��ԭ�ٶȷ��ظ��Եij����أ���֪![]() ��
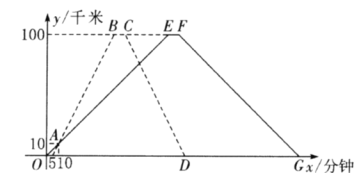
��![]() �������100ǧ��.�׳����ҳ���5���ӳ������׳�����10����ʱ��������ʻ��10ǧ�ף��ס�����������Գ����ص�·��
�������100ǧ��.�׳����ҳ���5���ӳ������׳�����10����ʱ��������ʻ��10ǧ�ף��ס�����������Գ����ص�·��![]() (ǧ��)��׳�����ʱ��
(ǧ��)��׳�����ʱ��![]() (����)�ĺ���ͼ����ͼ��ʾ.
(����)�ĺ���ͼ����ͼ��ʾ.
(1)�׳���![]() �س��������ʱ��ס���������һ������?
�س��������ʱ��ס���������һ������?
(2)�ҳ���![]() �س��������ʱ��ס�����������Գ����صľ������?
�س��������ʱ��ס�����������Գ����صľ������?
���𰸡�(1)�׳���![]() �س�������
�س�������![]() ���ӣ��ס���������һ�������� (2)�ҳ���
���ӣ��ס���������һ�������� (2)�ҳ���![]() �س�������
�س�������![]() ���ӣ��ס�����������Գ����صľ������.
���ӣ��ס�����������Գ����صľ������.
��������
��1��ֱ�����ô���ϵ�������ó�ֱ��AB�Ľ���ʽy=2x-10����OE�Ľ���ʽΪy=x�����������������꼴�ɣ�
��2�������������ֱ��CD�Ľ���ʽΪy=-2x+220����y=x������������⣬x=y=![]() ,�ɵ�
,�ɵ� ![]() ���ӣ�
���ӣ�
(1)��ֱ��AB�Ľ���ʽΪy=k1x+b1 ��
�ཫ(5,0)��(10,10)����ã�![]() ��
��
��ã�![]() ��
��
��ֱ��AB����ʽΪy=2x10.
��ֱ��OE�Ľ���ʽΪy=k2x,��(10,10)����ã�10k2=10��
��k2=1��
��ֱ��OE�Ľ���ʽΪy=x��
��������һ������ʱ,(2x10)+x=100��
��x=![]() .
.
�𣺼׳���M�س�����,����![]() ���Ӽס���������һ��������
���Ӽס���������һ��������
(2)�������100=2xB10
��xB=55
��xC=xB+5=60
�����֪xDxC=xB5
��xD=110��
��ֱ��CD�Ľ���ʽΪ![]() ��
��
��![]() ��
��
��![]() ��
��
��ֱ��CD�Ľ���ʽΪy=2x+220
��![]() ��
��
�� ��
��
��![]() .
.
���ҳ���M�س�����,�־���403���ӣ��ס�����������Գ����صľ������.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�ı���ABCD�Ǿ��Σ��Ѿ�����ֱ��AC�۵�����B���ڵ�E��������DE����DE��AC=3��5���� ![]() ��ֵΪ�� ��
��ֵΪ�� �� 
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����֪AD��BC��AB��EF��CD��EG���ҵ�E��ֱ��AD������F��H��G��ֱ��BC����EHƽ����FEG����A����D��110�㣬�߶�EH�ij��Dz�������ƽ����AD��BC֮��ľ��룿Ϊʲô��
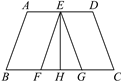
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���![]() ��ͼ��ֱ���
��ͼ��ֱ���![]() �ᡢ
�ᡢ![]() �ύ�ڵ�
�ύ�ڵ�![]() ��
��![]() �����߶�
�����߶�![]() Ϊ���ڵ�һ������������ֱ��������
Ϊ���ڵ�һ������������ֱ��������![]() ��
��![]() �����
�����![]() ��
��![]() �����ֱ�߶�Ӧ�ĺ�������ʽΪ________.
�����ֱ�߶�Ӧ�ĺ�������ʽΪ________.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2012�����У�����ǡ�ABC�У�AB=4��BC=5����ACB=45�㣬����ABC�Ƶ�B����ʱ�뷽����ת���õ���A1BC1 �� 
��1����ͼ1������C1���߶�CA���ӳ�����ʱ�����CC1A1�Ķ�����
��2����ͼ2������AA1 �� CC1 �� ����ABA1�����Ϊ4�����CBC1�������
��3����ͼ3����EΪ�߶�AB�е㣬��P���߶�AC�ϵĶ��㣬�ڡ�ABC�Ƶ�B����ʱ�뷽����ת�����У���P�Ķ�Ӧ���ǵ�P1 �� ���߶�EP1���ȵ����ֵ����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O����ABC��һ�㣬��A=80�㣬BO��CO�ֱ�����ABC����ACB�Ľ�ƽ���ߣ�����BOC���ڣ�������

A. 140�� B. 120�� C. 130�� D. ��ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���BAC=90�㣬AD�Ǹߣ�BE�����ߣ�CF�ǽ�ƽ���ߣ�CF��AD�ڵ�G����BE�ڵ�H������˵������ȷ�������_____��
�١�ABE�����������BCE��������ڡ�AFG=��AGF���ۡ�FAG=2��ACF����BH=CH��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ͼ��AB�ǰ�ԲO��ֱ������AD��BC�ཻ�ڵ�P����ô ![]() ���ڡ�BPD�ģ� ��
���ڡ�BPD�ģ� �� 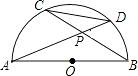
A.����
B.����
C.����
D.���϶�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������
��1����18������2����3
��2������![]() ��������90����
��������90����![]()
��3����2.5��![]() ������
������![]() ����
����
��4������10��2��[16+����3��2]
��5����![]() ��
��![]() +2����
+2����![]()
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com