
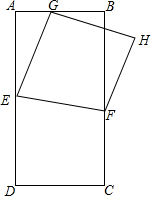
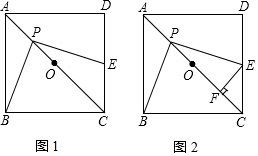
 矩形ABCD满足BC=2AB,E、F分别为AD、BC边上的动点,连接EF,沿EF将四边形DEFC翻折至四边形GEFH,点G落在AB上.
矩形ABCD满足BC=2AB,E、F分别为AD、BC边上的动点,连接EF,沿EF将四边形DEFC翻折至四边形GEFH,点G落在AB上.分析 (1)①如图1中,作FR⊥AD于R,连接DG.由△ADG∽△RFE,推出$\frac{AD}{RF}$=$\frac{AG}{RE}$=2,推出AG=2EF=2(DE-CF),推出$\frac{DE-CF}{AG}$=$\frac{1}{2}$.
②如图在中,作HJ⊥AB交AB的延长线于J.设EG=ED=x,在Rt△AEG中,由AG2+AE2=EG2,可得(4-x)2+12=x2,解得x=$\frac{17}{8}$,推出AE=AD-DE=4-$\frac{17}{8}$=$\frac{15}{8}$,由△AEG∽△JGH,可得$\frac{AE}{GJ}$=$\frac{AG}{JH}$=$\frac{EG}{GH}$,求出GJ、JH即可解决问题.
(2)如图2中,当点G与点B重合时,$\frac{CH}{BH}$的值最小,设DE=EB=a,AB=CD=BH=m,AD=BC=2m,在Rt△AEB中,由AE2+AB2=EB2,可得(2m-a)2+m2=a2,推出a=$\frac{5}{4}$m,推出DE=EB=$\frac{5}{4}$m,由AD∥BC,推出∠EFB=∠DEF=∠FEB,推出BE=BF=$\frac{5}{4}$m,CF=BC-BF=$\frac{3}{4}$m,设EF的延长线交CH于M.由△FMC∽△BAD,可得$\frac{FM}{CM}$=$\frac{BA}{AD}$=$\frac{1}{2}$,推出CM=KM=$\frac{3\sqrt{5}}{10}$m,推出CH=$\frac{3\sqrt{5}}{5}$m,延长即可解决问题.
解答 解:(1)①如图1中,作FR⊥AD于R,连接DG.
∵DG⊥EF,FR⊥ED,
∴∠EFR=∠ADR,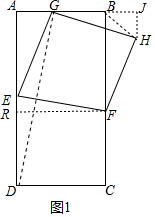
∴△ADG∽△RFE,
∴$\frac{AD}{RF}$=$\frac{AG}{RE}$=2,
∴AG=2EF=2(DE-CF),
∴$\frac{DE-CF}{AG}$=$\frac{1}{2}$.
②如图在中,作HJ⊥AB交AB的延长线于J.
∵AG=BG=1,
∴AB=CD=GH=2,AD=BC=4,设EG=ED=x,
在Rt△AEG中,∵AG2+AE2=EG2,
∴(4-x)2+12=x2,
∴x=$\frac{17}{8}$,
∴AE=AD-DE=4-$\frac{17}{8}$=$\frac{15}{8}$,
∵△AEG∽△JGH,
∴$\frac{AE}{GJ}$=$\frac{AG}{JH}$=$\frac{EG}{GH}$,
∴$\frac{\frac{15}{8}}{GJ}$=$\frac{1}{JH}$=$\frac{\frac{17}{8}}{2}$,
∴GJ=$\frac{30}{17}$,JH=$\frac{16}{17}$,
∴BJ=$\frac{13}{17}$,
∴BH=$\sqrt{B{J}^{2}+H{J}^{2}}$=$\sqrt{(\frac{13}{17})^{2}+(\frac{16}{17})^{2}}$=$\frac{5\sqrt{17}}{17}$
(2)如图2中,当点G与点B重合时,$\frac{CH}{BH}$的值最小,设DE=EB=a,AB=CD=BH=m,AD=BC=2m,
在Rt△AEB中,∵AE2+AB2=EB2,
∴(2m-a)2+m2=a2,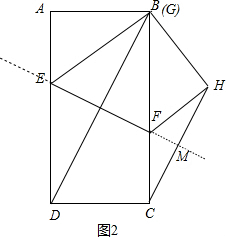
∴a=$\frac{5}{4}$m,
∴DE=EB=$\frac{5}{4}$m,
∵AD∥BC,
∴∠EFB=∠DEF=∠FEB,
∴BE=BF=$\frac{5}{4}$m,CF=BC-BF=$\frac{3}{4}$m,设EF的延长线交CH于M.
∵△FMC∽△BAD,
∴$\frac{FM}{CM}$=$\frac{BA}{AD}$=$\frac{1}{2}$,
∴CM=KM=$\frac{3\sqrt{5}}{10}$m,
∴CH=$\frac{3\sqrt{5}}{5}$m,
∴$\frac{CH}{BH}$的最小值=$\frac{3\sqrt{5}}{5}$.
点评 本题考查相似三角形综合题、翻折变换、勾股定理、相似三角形的判定和性质、等腰三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,构造相似三角形,学会利用特殊位置解决最值问题,属于中考压轴题.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
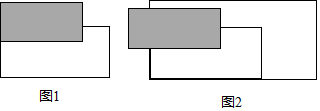
| A. | (m+a)(n+b) | B. | m(n+b)+a(n+b) | C. | mn+b(m+a)+a(n+b) | D. | mn+bm+an+ab |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标中,抛物线y=ax2+bx+3与x轴分别交于点A(2,0)、点B(点B在点A右侧),与y轴交于点C,tan∠CBA=$\frac{1}{2}$.
在平面直角坐标中,抛物线y=ax2+bx+3与x轴分别交于点A(2,0)、点B(点B在点A右侧),与y轴交于点C,tan∠CBA=$\frac{1}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com