
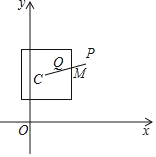
����Ŀ����ƽ��ֱ������ϵxOy�У�����Ϊ��C�����εĸ��߷ֱ�����������ƽ�У�����P����C���غϵĵ㣬��P���������εķ����Q�Ķ������£�������CP�������εı��ڵ�M��������CP�ϴ���һ��Q������CP+CQ��2CM�����QΪ��P���������εķ������ͼΪ��P���������εķ����Q��ʾ��ͼ��
�ر�أ�����P������C�غ�ʱ���涨CP��0��
��1���������ε�����Ϊԭ��O���߳�Ϊ2ʱ��
�ٷֱ��жϵ�F��2��0����G��![]() ��
��![]() ����H��3��3�����ڸ������εķ�����Ƿ���ڣ������ڣ�ֱ��д������������ꣻ
����H��3��3�����ڸ������εķ�����Ƿ���ڣ������ڣ�ֱ��д������������ꣻ
������P��ֱ��y����x+3�ϣ��ҵ�P���ڸ������εķ����Q���ڣ����P�ĺ������ȡֵ��Χ��
��2���������ε�����C��x���ϣ��߳�Ϊ2��ֱ��y��![]() ��x�ᡢy��ֱ��ڵ�A��B�����߶�AB�ϴ��ڵ�P��ʹ�õ�P���ڸ������εķ����Q�������ε��ڲ���ֱ��д�������ε�����C�ĺ������ȡֵ��Χ��
��x�ᡢy��ֱ��ڵ�A��B�����߶�AB�ϴ��ڵ�P��ʹ�õ�P���ڸ������εķ����Q�������ε��ڲ���ֱ��д�������ε�����C�ĺ������ȡֵ��Χ��
���𰸡���1���ٵ� F �ķ��������Ϊ��0��0������ G �ķ��������Ϊ����![]() ��
��![]() �����ڵ� P ��ֱ�� y=��x+3 �ϣ��ҵ� P ���ڸ������εķ���� Q ���ڣ��� P �ĺ������ȡֵ��Χ1��x��2����2�����������������ε����� C �ĺ������ȡֵ��ΧΪ 4��2
�����ڵ� P ��ֱ�� y=��x+3 �ϣ��ҵ� P ���ڸ������εķ���� Q ���ڣ��� P �ĺ������ȡֵ��Χ1��x��2����2�����������������ε����� C �ĺ������ȡֵ��ΧΪ 4��2![]() ��x��5��
��x��5��![]() �� 7��
�� 7��![]() ��x��8��
��x��8��
��������
��1���ٸ��ݵ�P���������εķ����Ķ����֪��������������ABCD���߳�Ϊ4������Ϊԭ��O�����ڲ�ʱ�����������εı��ϣ��з���㣬�۲�ͼ���֪����F����G�з���㣬���ݶ��弴�ɽ�����⣻
����ͼ2�У�ֱ��y=-x+3��CD��K��1��2������BC��H��2��1�����۲�ͼ���жϣ�
��2����ͼ3�У�������A��0��2![]() ����B��6��0��������ĸ�����λ�õĵ�C�����꼴���жϣ�
����B��6��0��������ĸ�����λ�õĵ�C�����꼴���жϣ�
��1������ͼ 1 �У�
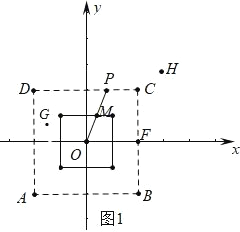
���ݵ�P ���������εķ����Ķ����֪�������������� ABCD���߳�Ϊ 4 ����Ϊԭ�� O�����ڲ�ʱ�����������εı��ϣ����з���㣬
�۲�ͼ���֪���� F���� G �з���㣬
�� F �ķ��������Ϊ��0��0������ G �ķ��������Ϊ����![]() ��
��![]() ����
����
����ͼ 2 �У�
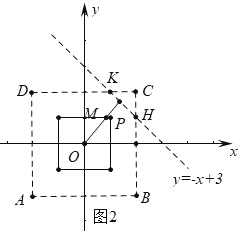
��ͼֱ�� y=��x+3 �� CD �� K��1��2������ BC �� H��2��1����
��� P ��ֱ�� y=��x+3 �ϣ��ҵ� P ���ڸ������εķ���� Q ���ڣ��� P �ĺ������ȡֵ��ΧΪ 1��x��2��
��2����ͼ 3 �У������� A��0��2![]() ����B��6��0����
����B��6��0����
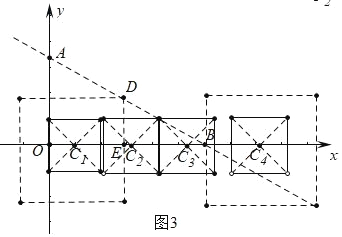
�ɣ�1����֪���߳�Ϊ 4 �������εĶ��� D ���߶� AB ��ʱ��DE=2��
��DE��OA��
��![]() ��
��
��![]() ��
��
��EB=2![]() ��OE=6��2
��OE=6��2![]() ��
��
��OC1=6��2![]() ��2=4��2
��2=4��2![]() ��
��
��C1��4��2![]() ��
��
���߳�Ϊ 2 �Ķ������߶� AB ��ʱ��C2��5��![]() ��0����C3��7��
��0����C3��7��![]() �������߳�Ϊ 4 �������εı߾����� B ʱ���ɵ� C4��8��0����
�������߳�Ϊ 4 �������εı߾����� B ʱ���ɵ� C4��8��0����
�۲�ͼ���֪�����������������ε����� C �ĺ������ȡֵ��ΧΪ 4��2![]() ��x��5��
��x��5�� ![]() �� 7��
�� 7��![]() ��x��8��
��x��8��


 �ܿ�����ĩ��̾�ϵ�д�
�ܿ�����ĩ��̾�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() �У�
��![]() ��
��![]() ��
��![]() ��ƽ����
��ƽ����![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() ƽ��
ƽ��![]() ���������н��ۣ���
���������н��ۣ���![]() ����
����![]() ����
����![]() ����
����![]() ����
����![]() ��������ȷ�Ľ�����______��
��������ȷ�Ľ�����______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
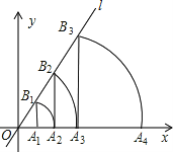
����Ŀ����ֱ������ϵ�У�ֱ��lΪy=![]() x������A1��1��0����A1B1��x�ᣬ��ֱ��l���ڵ�B1����ԭ��OΪԲ�ģ�OB1��Ϊ�뾶������x���ڵ�A2������A2B2��x�ᣬ��ֱ��l�ڵ�B2����ԭ��OΪԲ�ģ�OB2��Ϊ�뾶������x���ڵ�A3����������������������ȥ�����A20��������______��
x������A1��1��0����A1B1��x�ᣬ��ֱ��l���ڵ�B1����ԭ��OΪԲ�ģ�OB1��Ϊ�뾶������x���ڵ�A2������A2B2��x�ᣬ��ֱ��l�ڵ�B2����ԭ��OΪԲ�ģ�OB2��Ϊ�뾶������x���ڵ�A3����������������������ȥ�����A20��������______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧ���ϣ�С����������һ�����⣺
��ͼ1���ڵ���![]() �У�
��![]() ��
��![]() ��
��![]() ����֤
����֤![]() ��
��
�ڴ�����Ļ����ϣ���ʦ���䣺
����![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() �ڵ�
�ڵ�![]() ����̽���߶�
����̽���߶�![]() ��
��![]() ��
��![]() ֮���������ϵ����˵�����ɣ�
֮���������ϵ����˵�����ɣ�
С��ͨ���о����֣�![]() ��
��![]() ��ij��������ϵ��
��ij��������ϵ��
С��ͨ���о����֣��������߶��е������ŵ�ͬһ��ֱ���ϣ������س�����������ͨ����һ�����������Եó����ۣ�
�Ķ�������ϣ���ش��������⣺
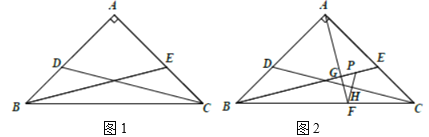
��1����֤![]() ��
��
��2������![]() ��
��![]() ��������ϵ����֤����
��������ϵ����֤����
��3��̽���߶�![]() ��
��![]() ��
��![]() ֮���������ϵ����֤����
֮���������ϵ����֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
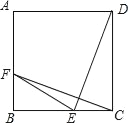
����Ŀ����ͼ����֪������ABCD����E��BC���ϣ�����DCE��ij��G��ת�õ���CBF����Fǡ����AB���ϣ�
��1���뻭����ת����G ��������ͼ�ۼ�����������GF��GE��
��2���������εı߳�Ϊ2a����CE���� ��ʱ��S��FGE��S��FBE����CE���� �� ʱ��S��FGE��3S��FBE��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
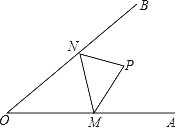
����Ŀ����ͼ����P�ǡ�AOB������һ�㣬�ҡ�AOB=40������M�͵�N�ֱ�������OA������OB�ϵĶ��㣬����PMN�ܳ�ȡ��Сֵʱ�����MPN�Ķ���Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
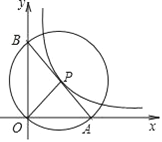
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�O Ϊ����ԭ�㣬P�Ƿ���������![]() ͼ��������һ�㣬��PΪԲ�ģ�POΪ�뾶��Բ��x�ύ�ڵ� A����y�ύ�ڵ�B������AB��
ͼ��������һ�㣬��PΪԲ�ģ�POΪ�뾶��Բ��x�ύ�ڵ� A����y�ύ�ڵ�B������AB��
��1����֤��PΪ�߶�AB���е㣻
��2������AOB�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
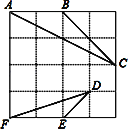
����Ŀ����ͼ����4��4�������η����У���ABC����DEF�Ķ��㶼�ڱ߳�Ϊ1��С�����εĶ����ϣ�
����գ���ABC=�� ���㣬AC=�� ����
���жϣ���ABC����DEF�Ƿ����ƣ���֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
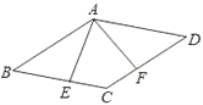
����Ŀ��������ABCD�У�AE��BC��AF��CD�� ��E��F�ֱ�ΪBC��CD���е㣬����EAF ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com