
分析 先将各个式子拆分,再抵消即可求解.
解答 解:$\frac{1}{1×2}$+$\frac{1}{3×2}$+$\frac{1}{4×3}$+…+$\frac{1}{2016×2015}$
=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{2015}$-$\frac{1}{2016}$
=1-$\frac{1}{2016}$
=$\frac{2015}{2016}$.
点评 考查了有理数混合运算,有理数混合运算的四种运算技巧:1.转化法:一是将除法转化为乘法,二是将乘方转化为乘法,三是在乘除混合运算中,通常将小数转化为分数进行约分计算. 2.凑整法:在加减混合运算中,通常将和为零的两个数,分母相同的两个数,和为整数的两个数,乘积为整数的两个数分别结合为一组求解. 3.分拆法:先将带分数分拆成一个整数与一个真分数的和的形式,然后进行计算. 4.巧用运算律:在计算中巧妙运用加法运算律或乘法运算律往往使计算更简便.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
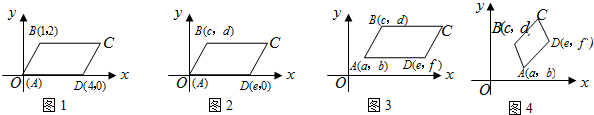
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com