
分析 (1)直接利用平方差公式分解因式得出答案;
(2)直接利用平方差公式分解因式得出答案;
(3)直接利用平方差公式分解因式得出答案;
(4)直接利用平方差公式分解因式得出答案;
(5)首先提取公因式3a,进而利用平方差公式分解因式得出答案;
(6)直接利用平方差公式分解因式得出答案.
解答 解:(1)(m+n)2-n2
=(m+n-n)(m+n+n)
=m(m+2n);
(2)49(a-b)2-16(a+b)2
=[7(a-b)-4(a+b)][7(a-b)+4(a+b)]
=(3a-11b)(11a-3b);
(3)(2x+y)2-(x+2y)2
=(2x+y+x+2y)(2x+y-x-2y)
=3(x+y)(x-y);
(4)(x2+y2)2-x2y2
=(x2+y2-xy)(x2+y2+xy);
(5)3ax2-3ay4
=3a(x2-y4)
=3a(x-y2)(x+y2);
(6)p4-1=(p2+1)(p2-1)
=(p2+1)(p-1)(p+1).
点评 此题主要考查了提取公因式法以及公式法分解因式,正确应用平方差公式是解题关键.


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案 培优三好生系列答案
培优三好生系列答案科目:初中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
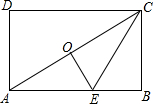 如图,已知矩形ABCD中,点E在AB上,点O是对角线AC的中点,沿CE折叠后,点B恰好与点O重合,若BC=6,则折痕CE的长为( )
如图,已知矩形ABCD中,点E在AB上,点O是对角线AC的中点,沿CE折叠后,点B恰好与点O重合,若BC=6,则折痕CE的长为( )| A. | 2$\sqrt{3}$ | B. | 4$\sqrt{3}$ | C. | 8 | D. | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
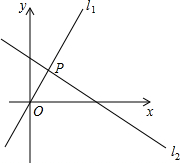 如图,直线l1过原点,直线l2解析式为y=-$\frac{\sqrt{3}}{3}$x+2,且直线l1和l2互相垂直,那么直线l1解析式为( )
如图,直线l1过原点,直线l2解析式为y=-$\frac{\sqrt{3}}{3}$x+2,且直线l1和l2互相垂直,那么直线l1解析式为( )| A. | y=$\frac{1}{3}$x | B. | y=$\frac{\sqrt{3}}{3}$x | C. | y=$\frac{\sqrt{3}}{2}$x | D. | y=$\sqrt{3}$x |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com