
分析 (1)根据规定M(5)=(-2)×(-2)×(-2)×(-2)×(-2),M(6)=(-2)×(-2)×(-2)×(-2)×(-2)×(-2),再按照运算法则运算即可;
(2)根据规定,2×M(2015)+M(2016))=2×$\underset{\underbrace{(-2)×(-2)×(-2)×…×(-2)}}{2015个(-2)相乘}$+$\underset{\underbrace{(-2)×(-2)×(-2)×…(-2)}}{2016个(-2)相乘}$,然后运算即可.
(3)当n为奇数时,则n+1为偶数,2×M(n)为-2n+1,M(n+1)为2n+1,可得2×M(n)+M(n+1)=0,可得结论;
当n为偶数时,则n+1为奇数,2×M(n)为2n+1,M(n+1)为-2n+1,可得2×M(n)+M(n+1)=0,可得结论.
解答 (1)解:根据规定可得,
M(5)=(-2)×(-2)×(-2)×(-2)×(-2),M(6)=(-2)×(-2)×(-2)×(-2)×(-2)×(-2),
∴M(5)+M(6)=(-2)×(-2)×(-2)×(-2)×(-2)+(-2)×(-2)×(-2)×(-2)×(-2)×(-2)
=(-2)5+26
=-25+26
=25;
(2)解:根据规定,
2×M(2015)+M(2016))=2×$\underset{\underbrace{(-2)×(-2)×(-2)×…×(-2)}}{2015个(-2)相乘}$+$\underset{\underbrace{(-2)×(-2)×(-2)×…(-2)}}{2016个(-2)相乘}$,
=2×(-22015)+22016
=-22016+22016
=0;
(3)证明:当n为奇数时,则n+1为偶数,
2×M(n)=-2n+1,M(n+1)=2n+1,
∴2×M(n)+M(n+1)=0,
∴2×M(n)与 M(n+1)互为相反数;
当n为偶数时,则n+1为奇数,
2×M(n)=2n+1,M(n+1)=-2n+1,
∴2×M(n)+M(n+1)=0,
∴2×M(n)与 M(n+1)互为相反数.
点评 本题主要考查了新定义运算和有理数的混合运算,掌握规律是解答此题的关键.


 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
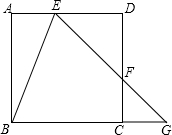 如图,正方形ABCD中,E,F分别在AD,DC上,EF的延长线交BC的延长线于G点,且∠AEB=∠BEG;
如图,正方形ABCD中,E,F分别在AD,DC上,EF的延长线交BC的延长线于G点,且∠AEB=∠BEG;查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
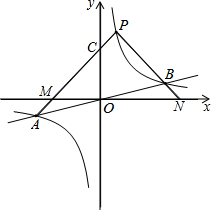 如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=$\frac{1}{4}$x的图象交于点A、B.点B的横坐标是4.点P是第一象限内反比例函数图象上的动点,且在直线AB的上方.
如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=$\frac{1}{4}$x的图象交于点A、B.点B的横坐标是4.点P是第一象限内反比例函数图象上的动点,且在直线AB的上方.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com