
【题目】如图,在平面直角坐标系中,![]() ,点
,点![]() 为
为![]() 轴正半轴上一动点,连接
轴正半轴上一动点,连接![]() ,将
,将![]() 沿
沿![]() 翻折得
翻折得![]() ,点
,点![]() 分别为
分别为![]() 的中点,连接
的中点,连接![]() 并延长交
并延长交![]() 所在直线于点
所在直线于点![]() ,连接
,连接![]() .当
.当![]() 为直角三角形时,点
为直角三角形时,点![]() 坐标为_______.
坐标为_______.
【答案】![]() 或
或![]()
【解析】
证出CD是△AOB的中位线,得出CE∥OB,由折叠的性质得出∠AO′B=∠AOB=90°,分两种情况:①当∠O′ED=90°时,则O′B⊥OB,四边形AOBO′是正方形,得出OC=CD=1,得出点D坐标为:(1,1);
②当∠O′DE=90°时,过点D作DN⊥OB于N,证明Rt△O'DE∽Rt△BO′A,得出∠O′ED=∠BAO′,由平行线的性质得出∠O′ED=∠O′BO=2∠O′BA=2∠ABO,由得出的性质得出△ABO≌△ABO′,得出∠OAB=∠O′AB=2∠ABO,则∠ABO=30°,由直角三角形的性质得出BD=2,由勾股定理得出OB=![]() =2
=2![]() ,得出DN=
,得出DN=![]() BD=1,BN=
BD=1,BN=![]() =
=![]() ,求出ON=OB-BN=2
,求出ON=OB-BN=2![]() -
-![]() =
=![]() ,得出点D坐标为:(
,得出点D坐标为:(![]() ,1)即可.
,1)即可.
∵点C,D分别为AO,AB的中点,
∴CD是△AOB的中位线,
∴CE∥OB,
∵△ABO沿AB翻折得到△ABO',
∴∠AO′B=∠AOB=90°,
∴当△O'DE为直角三角形时,∠O′ED=90°或∠O′DE=90°,
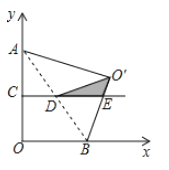
①当∠O′ED=90°时,如图1所示:
则O′B⊥OB,四边形AOBO′是正方形,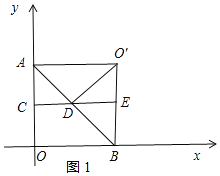
∵A(0,2),
∴OC=CD=1,
∴点D坐标为:(1,1);
②当∠O′DE=90°时,过点D作DN⊥OB于N,如图2所示:
∵点D是AB的中点,
∴O′D=BD,
∴∠DO′E=∠DBO′,
∵∠O′DE=∠AO′B=90°,
∴Rt△O'DE∽Rt△BO′A,
∴∠O′ED=∠BAO′,
∵CE∥OB,
∴∠O′ED=∠O′BO=2∠O′BA=2∠ABO,
∵△ABO与△ABO′关于直线AB对称,
∴△ABO≌△ABO′,
∴∠OAB=∠O′AB=2∠ABO,
∴∠ABO=30°,
∵A(0,2),
∴OA=2,
∴AB=4,
∴BD=2,OB=![]() ,
,
∴DN=![]() BD=1,BN=
BD=1,BN=![]() ,
,
∴ON=OB-BN=2![]() -
-![]() =
=![]() ,
,
∴点D坐标为:(![]() ,1);
,1);
综上所述,点D坐标为:(1,1)或(![]() ,1);
,1);
故答案为:(1,1)或(![]() ,1).
,1).


科目:初中数学 来源: 题型:
【题目】现如今,“垃圾分类”意识已深入人心,垃圾一般可分为:可回收物、厨余垃圾、有害垃圾、其它垃圾.其中甲拿了一袋垃圾,乙拿了两袋垃圾.
(1)直接写出甲所拿的垃圾恰好是“厨余垃圾”的概率;
(2)求乙所拿的两袋垃圾不同类的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
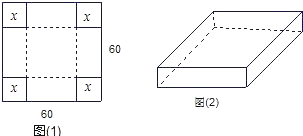
【题目】用一块边长为60㎝的正方形薄钢片制作一个长方体盒子:如果要做成一个没有盖的长方体盒子,可先在薄钢片的四个角上截去四个相同的小正方形,如图(1),然后把四边折合起来,如图(2)
(1)求做成的盒子底面积y(㎝2)与截去小正方形边长x(㎝)之间的函数关系式;
(2)当做成的盒子的底面积为900㎝2时,试求该盒子的容积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在正方形ABCD中,点E、F分别在BC和CD上,AE = AF

(1)求证:BE = DF;
(2)连接AC交EF于点O,延长OC至点M,使OM = OA,连接EM、FM.判断四边形AEMF是什么特殊四边形?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
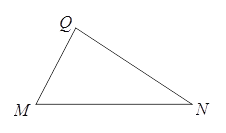
【题目】已知:如图,△MNQ中,MQ≠NQ.
(1)请你以MN为一边,在MN的同侧构造一个与△MNQ全等的三角形,画出图形,并简要说明构造的方法;
(2)参考(1)中构造全等三角形的方法解决下面问题:
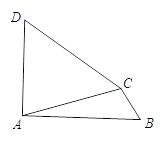
如图,在四边形ABCD中,![]() ,∠B=∠D.求证:CD=AB.
,∠B=∠D.求证:CD=AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等腰![]() 中,
中,![]() ,作
,作![]() 的平分线交
的平分线交![]() 于点
于点![]() ,将
,将![]() 绕点
绕点![]() 旋转,使
旋转,使![]() 的两边交直线
的两边交直线![]() 于点
于点![]() ,交直线
,交直线![]() 于点
于点![]() .
.
(1)当![]() 绕点
绕点![]() 旋转到如图①的位置时,请直接写出三条线段
旋转到如图①的位置时,请直接写出三条线段![]() 的数量关系;
的数量关系;
(2)当![]() 绕点
绕点![]() 旋转到如图②的位置时,(1)中结论是否成立,若成立,请证明;若不成立,请写出正确的结论,并说明理由;
旋转到如图②的位置时,(1)中结论是否成立,若成立,请证明;若不成立,请写出正确的结论,并说明理由;
(3)若![]() ,当
,当![]() 时,请直接写出线段
时,请直接写出线段![]() 的长度.
的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=kx2+(1﹣2k)x+1﹣3k与x轴有两个不同的交点A、B.
(1)求k的取值范围;
(2)证明该抛物线一定经过非坐标轴上的一点M,并求出点M的坐标;
(3)当![]() <k≤8时,由(2)求出的点M和点A,B构成的△ABM的面积是否有最值?若有,求出该最值及相对应的k值.
<k≤8时,由(2)求出的点M和点A,B构成的△ABM的面积是否有最值?若有,求出该最值及相对应的k值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某养殖公司准备运送152箱小龙虾到A、B两地销售,该批小龙虾刚好能用大小货车15辆一次运完,已知大货车每辆能装12箱,小货车每辆能装8箱,其中每辆大货车运往A、B两地的运费分别为800元和900元;每辆小货车运往A、B两地的运费分别为400元和600元.
(1)求这15辆车中大小货车各有多少辆?
(2)现安排其中10辆货车前往A地,其余货车前往B地,设前往A地的大货车为m辆,前往A、B两地总费用为y元,试求出y与m的函数解析式,并写出m的取值范围;
(3)在(2)的条件下,若运往B地的费用不高于A地费用的一半,求此时的最低总运费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y1=kx+1(k<0)与直线y2=mx(m>0)的交点坐标为(![]() ,
,![]() m),则不等式组mx﹣2<kx+1<mx的解集为( )
m),则不等式组mx﹣2<kx+1<mx的解集为( )
A. x>![]() B.
B. ![]() <x<
<x<![]() C. x<
C. x<![]() D. 0<x<
D. 0<x<![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com