
 ,CF⊥BD分别交BD、AD于点E、F,连接BF.
,CF⊥BD分别交BD、AD于点E、F,连接BF.
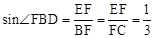 。
。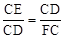 ,即:6x2=12,解得:x=
,即:6x2=12,解得:x=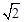 。
。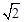 。
。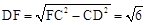 。
。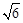 。
。

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源:不详 题型:解答题
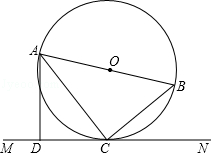
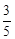 ,求⊙O的半径.
,求⊙O的半径.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 海里处,我海监船从A港口出发,自西向东航行至B处时,接上级命令赶赴C岛执行任务,此时C岛在B处北偏西45°方向上,海监船立刻改变航向以每小时60海里的速度沿BC行进,则从B处到达C岛需要多少小时?
海里处,我海监船从A港口出发,自西向东航行至B处时,接上级命令赶赴C岛执行任务,此时C岛在B处北偏西45°方向上,海监船立刻改变航向以每小时60海里的速度沿BC行进,则从B处到达C岛需要多少小时?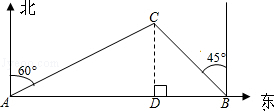
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
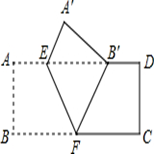
| A.12 | B.24 | C.12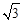 | D.16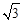 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
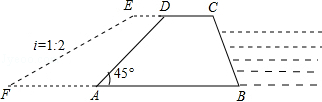
科目:初中数学 来源:不详 题型:解答题
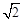 ≈1.41)
≈1.41)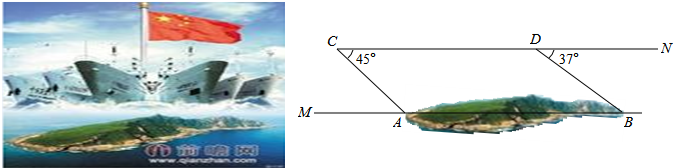
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com