
【题目】如图,在Rt△ABC中,∠ACB=90°,AB=4,BC=2,将△ABC绕点B顺时针方向旋转到△A′BC′的位置,此时点A′恰好在CB的延长线上,则图中阴影部分的面积为_____(结果保留π).
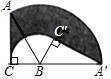
【答案】4π
【解析】由将△ABC绕点B顺时针方向旋转到△A′BC′的位置,此时点A′恰好在CB的延长线上,可得△ABC≌△A′BC′,由题给图可知:S阴影=S扇形ABA′+S△ABC﹣S扇形CBC′﹣S△A′BC′可得出阴影部分面积.
∵△ABC中,∠ACB=90°,AB=4,BC=2,
∴∠BAC=30°,∠ABC=60°,AC=2![]() ,
,
∵将△ABC绕点B顺时针方向旋转到△A′BC′的位置,此时点A′恰好在CB的延长线上,
∴△ABC≌△A′BC′,
∴∠ABA′=120°=∠CBC′,
∴S阴影=S扇形ABA′+S△ABC﹣S扇形CBC′﹣S△A′BC′
=S扇形ABA′﹣S扇形CBC′
=![]()
=4π,
故答案为:4π.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABD≌△CDB,且AB,CD是对应边.下面四个结论中不正确的是( )

A. △ABD和△CDB的面积相等B. △ABD和△CDB的周长相等
C. ∠A+∠ABD=∠C+∠CBDD. AD∥BC,且AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】渔夫在静水划船总是每小时5里,现在逆水行舟,水流速度是每小时3里;一阵风把他帽子吹落在水中,假如他没有发现,继续向前划行;等他发觉时人与帽子相距2.5里;

于是他立即原地调头追赶帽子,原地调转船头用了10分钟.
![]()
计算:
(1)求顺水速度,逆水速度是多少?
(2)从帽子丢失到发觉经过了多少时间?
(3)从发觉帽子丢失到捡回帽子经过了多少时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将长为10的线段OA绕点O旋转90°得到OB,点A的运动轨迹为![]() ,P是半径OB上一动点,Q是
,P是半径OB上一动点,Q是![]() 上的一动点,连接PQ.
上的一动点,连接PQ.
发现:∠POQ=________时,PQ有最大值,最大值为________;
思考:(1)如图2,若P是OB中点,且QP⊥OB于点P,求![]() 的长;
的长;
(2)如图3,将扇形AOB沿折痕AP折叠,使点B的对应点B′恰好落在OA的延长线上,求阴影部分面积;
探究:如图4,将扇形OAB沿PQ折叠,使折叠后的弧QB′恰好与半径OA相切,切点为C,若OP=6,求点O到折痕PQ的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算与化简
(1)(﹣2x)3x6÷(﹣3x3)2
(2)5m(m﹣n)﹣(5m+n)(m﹣n)
(3)利用简便方法计算:20202﹣2019×2021
(4)先化简,再求值:[(a+b)2﹣(a﹣b)(a+b)]÷(2b),其中a=﹣![]() ,b=﹣1.
,b=﹣1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课堂上,老师提出问题:如图,如何在该图形中数出黑色正方形的个数,以下是两位同学的做法:
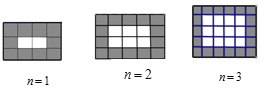
(1)甲同学的做法为:
当![]() 时,黑色正方形的个数共有
时,黑色正方形的个数共有![]()
当![]() 时,黑色正方形的个数共有
时,黑色正方形的个数共有![]()
当![]() 时,黑色正方形的个数共有
时,黑色正方形的个数共有![]()
……则在第![]() 个图形中,黑色正方形的个数共有 (无需化简)
个图形中,黑色正方形的个数共有 (无需化简)
(2)乙同学的做法为:
当![]() 时,黑色正方形的个数共有
时,黑色正方形的个数共有![]()
当![]() 时,黑色正方形的个数共有
时,黑色正方形的个数共有![]()
当![]() 时,黑色正方形的个数共有
时,黑色正方形的个数共有![]()
……则在第![]() 个图形中,黑色正方形的个数共有 (无需化简)
个图形中,黑色正方形的个数共有 (无需化简)
(3)数学老师及时肯定了两位同学的做法,从而可以得到等式
(4)请利用学习过的知识验证(3)问中的等式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:A、B两点在直线l的同一侧,线段AO,BM均是直线l的垂线段,且BM在AO的右边,AO=2BM,将BM沿直线l向右平移,在平移过程中,始终保持∠ABP=90°不变,BP边与直线l相交于点P.
(1)当P与O重合时(如图2所示),设点C是AO的中点,连接BC.求证:四边形OCBM是正方形;
(2)请利用如图1所示的情形,求证:![]() =
=![]() ;
;
(3)若AO=2![]() ,且当MO=2PO时,请直接写出AB和PB的长.
,且当MO=2PO时,请直接写出AB和PB的长.
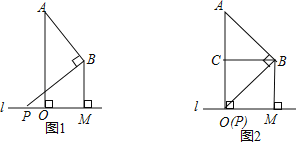
查看答案和解析>>
科目:初中数学 来源: 题型:
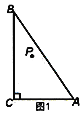
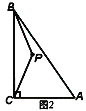
【题目】如图1.在△ABC中,∠ACB=90°,点P为△ABC内一点.
(1)连接PB、PC,将△BCP沿射线CA方向平移,得到△DAE,点B、C、P的对应点分别为点D、A、E,连接CE.
①依题意,请在图2中补全图形;
②如果BP⊥CE,AB+BP=9,CE=![]() ,求AB的长.
,求AB的长.
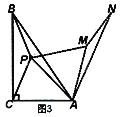
(2)如图3,以点A为旋转中心,将△ABP顺时针旋转60°得到△AMN,连接PA、PB、PC,当AC=4,AB=8时,根据此图求PA+PB+PC的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等边△ABC的边长是2,以BC边上的高AB1为边作等边三角形,得到第一个等边△AB1C1;再以等边△AB1C1的B1C1边上的高AB2为边作等边三角形,得到第二个等边△AB2C2;再以等边△AB2C2的B2C2边上的高AB3为边作等边三角形,得到第三个等边△AB3C3;…,记△B1CB2的面积为S1,△B2C1B3的面积为S2,△B3C2B4的面积为S3,如此下去,则Sn=_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com