
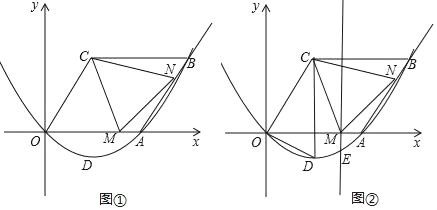
ĄžĚâÄżĄżČçÍźĹ×ÎďĎßy=ax2+bxŁŹšýľăAŁ¨4ŁŹ0ŁŠşÍľăBŁ¨6ŁŹ2![]() ŁŠŁŹËÄąßĐÎOCBAĘÇĆ˝ĐĐËÄąßĐÎŁŹľăMŁ¨tŁŹ0ŁŠÎŞxÖáŐý°ëÖáÉϾľ㣏ľăNÎŞÉäĎßABÉϾľ㣏ÇŇAN=OMŁŹľăDÎŞĹ×ÎďĎ߾ĜĽľăŁŽ
ŁŠŁŹËÄąßĐÎOCBAĘÇĆ˝ĐĐËÄąßĐÎŁŹľăMŁ¨tŁŹ0ŁŠÎŞxÖáŐý°ëÖáÉϾľ㣏ľăNÎŞÉäĎßABÉϾľ㣏ÇŇAN=OMŁŹľăDÎŞĹ×ÎďĎ߾ĜĽľăŁŽ
Ł¨1ŁŠÇóĹ×ÎďĎ߾ĽâÎöĘ˝ŁŹ˛˘Öą˝ÓĐ´łöľăDľÄ×řąęŁť
Ł¨2ŁŠľąĄ÷AMNľÄÖÜł¤×îĐĄĘąŁŹÇótľÄÖľŁť
Ł¨3ŁŠČçÍź˘ÚŁŹšýľăM×÷MEĄÍxÖᣏ˝ťĹ×ÎďĎßy=ax2+bxÓÚľăEŁŹÁŹ˝ÓEMŁŹAEŁŹľąĄ÷AMEÓëĄ÷DOCĎŕËĆĘąŁŽÇëÖą˝ÓĐ´łöËůÓСűşĎĚőźţľÄľăM×řąęŁŽ
Ąž´đ°¸ĄżŁ¨1ŁŠy=![]() x2Š
x2Š![]() xŁŹľăDľÄ×řąęÎŞŁ¨2ŁŹŠ
xŁŹľăDľÄ×řąęÎŞŁ¨2ŁŹŠ![]() ŁŠŁťŁ¨2ŁŠt=2ŁťŁ¨3ŁŠMľăľÄ×řąęÎŞŁ¨2ŁŹ0ŁŠťňŁ¨6ŁŹ0ŁŠŁŽ
ŁŠŁťŁ¨2ŁŠt=2ŁťŁ¨3ŁŠMľăľÄ×řąęÎŞŁ¨2ŁŹ0ŁŠťňŁ¨6ŁŹ0ŁŠŁŽ
Ąž˝âÎöĄż
Ł¨1ŁŠŔűÓĂ´ýś¨ĎľĘýˇ¨ÇóĹ×ÎďĎß˝âÎöĘ˝ŁťŔűÓĂĹ䡽ˇ¨°ŃŇť°ăĘ˝ťŻÎŞśĽľăĘ˝ľĂľ˝ľăDľÄ×řąęŁť
Ł¨2ŁŠÁŹ˝ÓACŁŹČçÍź˘ŮŁŹĎČźĆËăłöAB=4ŁŹÔňĹĐśĎĆ˝ĐĐËÄąßĐÎOCBAÎŞÁâĐÎŁŹÔŮÖ¤Ă÷Ą÷AOCşÍĄ÷ACBśźĘǾȹßČý˝ÇĐÎŁŹ˝Ó×ĹÖ¤Ă÷Ą÷OCMĄŐĄ÷ACNľĂľ˝CM=CNŁŹĄĎOCM=ĄĎACNŁŹÔňĹМϥ÷CMNÎŞľČąßČý˝ÇĐξþ˝MN=CMŁŹÓÚĘÇĄ÷AMNľÄÖÜł¤=OA+CMŁŹÓÉÓÚCMĄÍOAĘąŁŹCMľÄÖľ×îĐĄŁŹĄ÷AMNľÄÖÜł¤×îĐĄŁŹ´ÓśřľĂľ˝tľÄÖľŁť
Ł¨3ŁŠĎČŔűÓĂš´šÉś¨ŔíľÄÄ木ŔíÖ¤Ă÷Ą÷OCDÎŞÖą˝ÇČý˝ÇĐÎŁŹĄĎCOD=90ĄăŁŹÉčMŁ¨tŁŹ0ŁŠŁŹÔňEŁ¨tŁŹ![]() t2-
t2-![]() tŁŠŁŹ¸ůžÝĎŕËĆČý˝ÇĐÎľÄĹĐś¨ˇ˝ˇ¨ŁŹľą
tŁŠŁŹ¸ůžÝĎŕËĆČý˝ÇĐÎľÄĹĐś¨ˇ˝ˇ¨ŁŹľą![]() ĘąŁŹĄ÷AMEĄ×Ą÷CODŁŹź´|t-4|Łş4=|
ĘąŁŹĄ÷AMEĄ×Ą÷CODŁŹź´|t-4|Łş4=|![]() t2-
t2-![]() t |Łş
t |Łş![]() ŁŹľą
ŁŹľą![]() ĘąŁŹĄ÷AMEĄ×Ą÷DOCŁŹź´|t-4|Łş
ĘąŁŹĄ÷AMEĄ×Ą÷DOCŁŹź´|t-4|Łş![]() =|
=|![]() t2-
t2-![]() t |Łş4ŁŹČťşóˇÖąđ˝âžřśÔÖľˇ˝łĚżÉľĂľ˝śÔÓŚľÄMľăľÄ×řąęŁŽ
t |Łş4ŁŹČťşóˇÖąđ˝âžřśÔÖľˇ˝łĚżÉľĂľ˝śÔÓŚľÄMľăľÄ×řąęŁŽ
Ł¨1ŁŠ°ŃAŁ¨4ŁŹ0ŁŠşÍBŁ¨6ŁŹ2![]() ŁŠ´úČëy=ax2+bxľĂ
ŁŠ´úČëy=ax2+bxľĂ
![]() ŁŹ˝âľĂ
ŁŹ˝âľĂ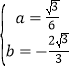 ŁŹ
ŁŹ
ĄŕĹ×ÎďĎß˝âÎöʽΪy=![]() x2-
x2-![]() xŁť
xŁť
Ąßy=![]() x2-
x2-![]() x =
x =![]() -2) 2-
-2) 2-![]() Łť
Łť
ĄŕľăDľÄ×řąęÎŞŁ¨2ŁŹ-![]() ŁŠŁť
ŁŠŁť
Ł¨2ŁŠÁŹ˝ÓACŁŹČçÍź˘ŮŁŹ

AB=![]() =4ŁŹ
=4ŁŹ
śřOA=4ŁŹ
ĄŕĆ˝ĐĐËÄąßĐÎOCBAÎŞÁâĐÎŁŹ
ĄŕOC=BC=4ŁŹ
ĄŕCŁ¨2ŁŹ2![]() ŁŠŁŹ
ŁŠŁŹ
ĄŕAC=![]() =4ŁŹ
=4ŁŹ
ĄŕOC=OA=AC=AB=BCŁŹ
ĄŕĄ÷AOCşÍĄ÷ACBśźĘǾȹßČý˝ÇĐÎŁŹ
ĄŕĄĎAOC=ĄĎCOB=ĄĎOCA=60ĄăŁŹ
śřOC=ACŁŹOM=ANŁŹ
ĄŕĄ÷OCMĄŐĄ÷ACNŁŹ
ĄŕCM=CNŁŹĄĎOCM=ĄĎACNŁŹ
ĄßĄĎOCM+ĄĎACM=60ĄăŁŹ
ĄŕĄĎACN+ĄĎACM=60ĄăŁŹ
ĄŕĄ÷CMNÎŞľČąßČý˝ÇĐÎŁŹ
ĄŕMN=CMŁŹ
ĄŕĄ÷AMNľÄÖÜł¤=AM+AN+MN=OM+AM+MN=OA+CM=4+CMŁŹ
ľąCMĄÍOAĘąŁŹCMľÄÖľ×îĐĄŁŹĄ÷AMNľÄÖÜł¤×îĐĄŁŹ´ËĘąOM=2ŁŹ
Ąŕt=2Łť
Ł¨3ŁŠĄßCŁ¨2ŁŹ2![]() ŁŠŁŹDŁ¨2ŁŹ-
ŁŠŁŹDŁ¨2ŁŹ-![]() ŁŠŁŹ
ŁŠŁŹ
ĄŕCD=![]() ŁŹ
ŁŹ
ĄßOD=![]() ŁŹOC=4ŁŹ
ŁŹOC=4ŁŹ
ĄŕOD2+OC2=CD2ŁŹ
ĄŕĄ÷OCDÎŞÖą˝ÇČý˝ÇĐÎŁŹĄĎCOD=90ĄăŁŹ
ÉčMŁ¨tŁŹ0ŁŠŁŹÔňEŁ¨tŁŹ![]() t2-
t2-![]() tŁŠŁŹ
tŁŠŁŹ
ĄßĄĎAME=ĄĎCODŁŹ
Ąŕľą![]() ĘąŁŹĄ÷AMEĄ×Ą÷CODŁŹź´|t-4|Łş4=|
ĘąŁŹĄ÷AMEĄ×Ą÷CODŁŹź´|t-4|Łş4=|![]() t2-
t2-![]() t |Łş
t |Łş![]() ŁŹ
ŁŹ
ŐűŔíľĂ|![]() t2-
t2-![]() t|=
t|=![]() |t-4|ŁŹ
|t-4|ŁŹ
˝âˇ˝łĚ![]() t2-
t2-![]() t =
t =![]() Ł¨t-4ŁŠľĂt1=4Ł¨ÉáČĽŁŠŁŹt2=2ŁŹ´ËĘąMľă×řąęÎŞŁ¨2ŁŹ0ŁŠŁť
Ł¨t-4ŁŠľĂt1=4Ł¨ÉáČĽŁŠŁŹt2=2ŁŹ´ËĘąMľă×řąęÎŞŁ¨2ŁŹ0ŁŠŁť
˝âˇ˝łĚ![]() t2-
t2-![]() t =-
t =-![]() Ł¨t-4ŁŠľĂt1=4Ł¨ÉáČĽŁŠŁŹt2=-2Ł¨ÉáČĽŁŠŁť
Ł¨t-4ŁŠľĂt1=4Ł¨ÉáČĽŁŠŁŹt2=-2Ł¨ÉáČĽŁŠŁť
ľą![]() ĘąŁŹĄ÷AMEĄ×Ą÷DOCŁŹź´|t-4|Łş
ĘąŁŹĄ÷AMEĄ×Ą÷DOCŁŹź´|t-4|Łş![]() =|
=|![]() t2-
t2-![]() t |Łş4ŁŹŐűŔíľĂ|
t |Łş4ŁŹŐűŔíľĂ|![]() t2-
t2-![]() t |=|t-4|ŁŹ
t |=|t-4|ŁŹ
˝âˇ˝łĚ![]() t2-
t2-![]() t =t-4ľĂt1=4Ł¨ÉáČĽŁŠŁŹt2=6ŁŹ´ËĘąMľă×řąęÎŞŁ¨6ŁŹ0ŁŠŁť
t =t-4ľĂt1=4Ł¨ÉáČĽŁŠŁŹt2=6ŁŹ´ËĘąMľă×řąęÎŞŁ¨6ŁŹ0ŁŠŁť
˝âˇ˝łĚ![]() t2-
t2-![]() t =-Ł¨t-4ŁŠľĂt1=4Ł¨ÉáČĽŁŠŁŹt2=-6Ł¨ÉáČĽŁŠŁť
t =-Ł¨t-4ŁŠľĂt1=4Ł¨ÉáČĽŁŠŁŹt2=-6Ł¨ÉáČĽŁŠŁť
×ŰÉĎËůĘöŁŹMľăľÄ×řąęÎŞŁ¨2ŁŹ0ŁŠťňŁ¨6ŁŹ0ŁŠŁŽ


 ÔÄśÁżěłľĎľÁĐ´đ°¸
ÔÄśÁżěłľĎľÁĐ´đ°¸
| Äęźś | ¸ßÖĐżÎłĚ | Äęźś | łőÖĐżÎłĚ |
| ¸ßŇť | ¸ßŇťĂâˇŃżÎłĚÍĆźöŁĄ | łőŇť | łőŇťĂâˇŃżÎłĚÍĆźöŁĄ |
| ¸ßśţ | ¸ßśţĂâˇŃżÎłĚÍĆźöŁĄ | łőśţ | łőśţĂâˇŃżÎłĚÍĆźöŁĄ |
| ¸ßČý | ¸ßČýĂâˇŃżÎłĚÍĆźöŁĄ | łőČý | łőČýĂâˇŃżÎłĚÍĆźöŁĄ |
żĆÄżŁşłőÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
ĄžĚâÄżĄżÔÚŇť´Î´ŮĎúťîśŻÖĐŁŹÄłÉĚłĄÎŞÁËÎüŇýšËżÍŁŹÉčÁ˘ÁËŇť¸öżÉŇÔ×ÔÓÉתśŻľÄתĹĚŁ¨ČçÍźŁŹ×ŞĹĚąťĆ˝žůˇÖłÉ![]() ˇÝŁŠŁŹ˛˘šćś¨ŁşšËżÍĂżšşÂň
ˇÝŁŠŁŹ˛˘šćś¨ŁşšËżÍĂżšşÂň![]() ÔŞľÄÉĚơŁŹžÍÄÜťńľĂŇť´ÎתśŻ×ŞĹ̾ĝúťáŁŽČçšűתĹĚÍŁÖšşóŁŹÖ¸ŐëŐýşĂśÔןşěÉŤĄ˘ťĆÉŤĄ˘ÂĚÉŤÇřÓňŁŹÄÇĂ´šËżÍžÍżÉŇÔˇÖąđťńľĂ
ÔŞľÄÉĚơŁŹžÍÄÜťńľĂŇť´ÎתśŻ×ŞĹ̾ĝúťáŁŽČçšűתĹĚÍŁÖšşóŁŹÖ¸ŐëŐýşĂśÔןşěÉŤĄ˘ťĆÉŤĄ˘ÂĚÉŤÇřÓňŁŹÄÇĂ´šËżÍžÍżÉŇÔˇÖąđťńľĂ![]() ÔŞĄ˘
ÔŞĄ˘![]() ÔŞĄ˘
ÔŞĄ˘![]() ÔŞľÄšşÎďČŻŁŹĆžšşÎďČŻżÉŇÔÔÚ¸ĂÉĚłĄźĚĐřšşÎČçšűšËżÍ˛ťÔ¸ŇâתתĹĚŁŹÄÇĂ´żÉŇÔÖą˝ÓťńľĂšşÎďČŻ
ÔŞľÄšşÎďČŻŁŹĆžšşÎďČŻżÉŇÔÔÚ¸ĂÉĚłĄźĚĐřšşÎČçšűšËżÍ˛ťÔ¸ŇâתתĹĚŁŹÄÇĂ´żÉŇÔÖą˝ÓťńľĂšşÎďČŻ![]() ÔŞŁŽ
ÔŞŁŽ
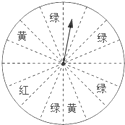
Ł¨1ŁŠÇóÿתśŻŇť´ÎתĹĚËůťńšşÎďČŻ˝đśîľÄĆ˝žůĘýŁť
Ł¨2ŁŠČçšűÄăÔÚ¸ĂÉĚłĄĎűˇŃ![]() ÔŞŁŹÄăťáŃĄÔńתתĹĚťšĘÇÖą˝ÓťńľĂšşÎďČŻŁżËľĂ÷ŔíÓÉŁŽ
ÔŞŁŹÄăťáŃĄÔńתתĹĚťšĘÇÖą˝ÓťńľĂšşÎďČŻŁżËľĂ÷ŔíÓÉŁŽ
˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁşłőÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
ĄžĚâÄżĄżź×ŁŹŇŇŁŹąűČýÖÖ×÷ÎˇÖąđÔÚÉ˝˝ĹŁŹÉ˝ŃüşÍÉ˝śĽČý¸öĘÔŃéĚď˝řĐĐĘÔŃ飏ÿ¸öĘÔŃéĚﲼÖÖśţĘŽÁŁÖÖ×ÓŁŹĹŠŇľ×¨źŇ˝ŤĂż¸öĘÔŃéĚďłÉťîľÄÖÖ×Ó¸öĘýÍłźĆČçĚőĐÎÍłźĆÍźŁŹČçÍźËůĘžŁŹĎÂĂćÓĐËĸöÍƜϣş
˘Ůź×ÖÖ×÷ÎďĘÜťˇžłÓ°Ďě×îĐĄŁť˘ÚŇŇÖÖ×÷ÎďĆ˝žůłÉťîÂĘ×î¸ßŁť
˘ŰąűÖÖ×÷Îď×îĘʺϲĽÖÖÔÚÉ˝ŃüŁť
˘ÜČçšűĂżÖÖ×÷ÎďÖťÄÜÔÚŇť¸öľŘˇ˝˛ĽÖÖŁŹÄÇĂ´É˝˝ĹŁŹÉ˝ŃüşÍÉ˝śĽˇÖąđ˛ĽÖ֟ףŹŇŇŁŹąűČýÖÖ×÷ÎďÄÜĘšľĂłÉťîÂĘ×î¸ßŁŽĆäÖĐşĎŔíľÄĘÇŁ¨ĄĄĄĄŁŠ

A. ˘Ů˘Ű B. ˘Ů˘Ü C. ˘Ú˘Ű D. ˘Ú˘Ü
˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁşłőÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
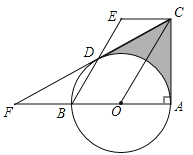
ĄžĚâÄżĄżČçÍźŁŹABĘÇĄŃOľÄÖąžśŁŹĄĎBAC=90ĄăŁŹËÄąßĐÎEBOCĘÇĆ˝ĐĐËÄąßĐÎŁŹEB˝ťĄŃOÓÚľăDŁŹÁŹ˝ÓCD˛˘ŃÓł¤˝ťABľÄŃÓł¤ĎßÓÚľăFŁŽ
Ł¨1ŁŠÇóÖ¤ŁşCFĘÇĄŃOľÄÇĐĎߣť
Ł¨2ŁŠČôĄĎF=30ĄăŁŹEB=6ŁŹÇóÍźÖĐŇőÓ°˛żˇÖľÄĂćťýŁ¨˝ášűąŁÁô¸ůşĹşÍŚĐŁŠ
˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁşłőÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
ĄžĚâÄżĄżÔÚŇť¸ö˛ťÍ¸Ă÷ľÄşĐ×ÓŔď×°ÓĐÖťÓĐŃŐÉŤ˛ťÍŹľÄşÚĄ˘°×Á˝ÖÖÇňš˛40¸öŁŹĐĄŔî×öĂţÇňĘÔŃ飏Ëý˝ŤşĐ×ÓŔďĂćľÄÇň˝ÁÔČşó´ÓÖĐËćťúĂţłöŇť¸öÇňźÇĎÂŃŐÉŤŁŹÔŮ°ŃËüˇĹťŘşĐ×ÓÖĐŁŹ˛ťśĎÖظ´ÉĎĘöšýłĚŁŹĎÂąíĘÇĘÔŃéÖĐľÄŇť×éÍłźĆĘýžÝŁş
ĂţÇňľÄ´ÎĘýn | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
Ăţľ˝°×ÇňľÄ´ÎĘým | 63 | 124 | 178 | 302 | 488 | 600 | 1800 |
Ăţľ˝°×ÇňľÄĆľÂĘ | 0.63 | 0.62 | 0.593 | 0.604 | 0.61 | ĄĄ ĄĄ | ĄĄ ĄĄ |
Ł¨1ŁŠÍęłÉÉĎąíŁť
Ł¨2ŁŠČô´ÓşĐ×ÓÖĐËćťúĂţłöŇť¸öÇňŁŹÔňĂţľ˝°×ÇňľÄ¸ĹÂĘPŁ˝ĄĄ ĄĄŁťŁ¨˝ášűąŁÁôĐĄĘýľăşóҝΝŁŠ
Ł¨3ŁŠšŔËăŐâ¸ö˛ťÍ¸Ă÷ľÄşĐ×ÓŔď°×ÇňÓĐśŕÉٸöŁż
˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁşłőÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
ĄžĚâÄżĄżČôĘýaĘššŘÓÚxľÄˇÖĘ˝ˇ˝łĚ![]() ľÄ˝âÎŞŐýĘýŁŹĘššŘÓÚyľÄ˛ťľČĘ˝×é
ľÄ˝âÎŞŐýĘýŁŹĘššŘÓÚyľÄ˛ťľČĘ˝×é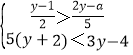 Î޽⣏ÔňËůÓĐÂú×ăĚőźţľÄŐűĘýaľÄÖľÖŽťýĘÇŁ¨ĄĄĄĄŁŠ
Î޽⣏ÔňËůÓĐÂú×ăĚőźţľÄŐűĘýaľÄÖľÖŽťýĘÇŁ¨ĄĄĄĄŁŠ
A. 360 B. 90 C. 60 D. 15
˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁşłőÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
ĄžĚâÄżĄż´ÓŠ2ŁŹŠ1ŁŹ0ŁŹ1ŁŹ2ŁŹ3ŐâÁů¸öĘýÖĐŁŹČÎČĄŇť¸öĘý×÷ÎŞaľÄÖľŁŹÇĄşĂĘšľĂšŘÓÚxĄ˘yľÄśţÔŞŇť´Îˇ˝łĚ×é![]() ÓĐŐűĘý˝âŁŹÇҡ˝łĚax2+ax+1=0ÓĐĘľĘý¸ůľÄ¸ĹÂĘĘÇ_____ŁŽ
ÓĐŐűĘý˝âŁŹÇҡ˝łĚax2+ax+1=0ÓĐĘľĘý¸ůľÄ¸ĹÂĘĘÇ_____ŁŽ
˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁşłőÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
ĄžĚâÄżĄżČçÍźŁŹČń˝ÇĄ÷ABCÖĐŁŹADĘǸߣŹE,FˇÖąđĘÇAB,ACÖĐľă,EF˝ťADÓÚG,ŇŃÖŞGF=1,AC= 6,Ą÷DEGľÄÖÜł¤ÎŞ10ŁŹÔňĄ÷ABCľÄÖÜł¤ÎŞŁ¨ ŁŠ

A. 27-3![]() B. 28-3
B. 28-3![]() C. 28-4
C. 28-4![]() D. 29-5
D. 29-5![]()
˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁşłőÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
ĄžĚâÄżĄżÖ¸łöĎÂÁĐÎĘĚâÖĐľÄ×ÜĚ奢¸öĚ奢ŃůąžŁş
Ł¨1ŁŠÎŞÁËšŔźĆÄłżéÓńĂ×ĘÔŃéĚďŔďľÄľĽÖęĆ˝žů˛úÁżŁŹ´ÓÖĐłéČĄ![]() Öę˝řĐĐĘľ˛âŁť
Öę˝řĐĐĘľ˛âŁť
Ł¨2ŁŠÄłŃ§ĐŁÎŞÁËÁË˝âѧÉúÍęłÉżÎÍâ×÷ŇľľÄĘąźäŁŹ´ÓÖĐłéŃůľ÷˛éÁË![]() ĂűѧÉúÍęłÉżÎÍâ×÷ŇľľÄĘąźä˝řĐСÖÎö.
ĂűѧÉúÍęłÉżÎÍâ×÷ŇľľÄĘąźä˝řĐСÖÎö.
˛éż´´đ°¸şÍ˝âÎö>>
°ŮśČÖÂĐĹ - ÁˇĎ°˛áÁĐąí - ĘÔĚâÁĐąí
şţąąĘĄťĽÁŞÍřÎĽˇ¨şÍ˛ťÁźĐĹϢžŮą¨Ć˝Ě¨ | ÍřÉĎÓĐşŚĐĹϢžŮą¨×¨Çř | ľçĐĹՊƞٹ¨×¨Çř | ÉćŔúʡĐéÎŢÖ÷ŇĺÓĐşŚĐĹϢžŮą¨×¨Çř | ÉćĆóÇÖȨžŮą¨×¨Çř
ÎĽˇ¨şÍ˛ťÁźĐĹϢžŮą¨ľçť°Łş027-86699610 žŮą¨ÓĘĎ䣺58377363@163.com