
 如图,已知?ABCD和?ABEF,连接AC、DF、CE、AE,AC与DF交于点G,若AC=DF=AE.
如图,已知?ABCD和?ABEF,连接AC、DF、CE、AE,AC与DF交于点G,若AC=DF=AE.分析 (1)直接利用平行四边形的性质和判定方法得出四边形FDCE是平行四边形,进而得出DF=EC,再利用已知求出答案;
(2)利用等边三角形的性质结合平行四边形的性质得出答案;
(3)利用等边三角形的性质结合平行四边形的对角线互相平分,进而得出AE⊥BF,即可得出答案.
解答 (1)证明:∵在?ABCD和?ABEF中,
∴AB$\stackrel{∥}{=}$EF,AB$\stackrel{∥}{=}$DC,
∴EF$\stackrel{∥}{=}$DC,
∴四边形FDCE是平行四边形,
∴FD=EC,
∵AC=DF=AE,
∴AE=AC=EC,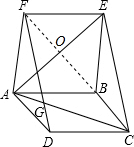
∴△AEC为等边三角形;
(2)解:∵△AEC为等边三角形,
∴∠ECA=60°,
∵四边形FDCE是平行四边形,
∴DF∥EC,
∴∠FGA=∠ECA=60°;
(3)证明:如图所示:连接FB,AE与BF相交于点O,
∵四边形ABEF是平行四边形,
∴AO=EO,
又∵△AEC为等边三角形,点F、B、C在同一直线上,
∴CO⊥AE,
∴AE⊥BF,
∴平行四边形ABEF是菱形.
点评 此题主要考查了平行四边形的判定与性质以及等边三角形的判定与性质,正确应用平行四边形的性质是解题关键.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在边长为1个单位长度的小正方形组成的网格中.
如图,在边长为1个单位长度的小正方形组成的网格中.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若矩形的面积为16$\sqrt{3}$,AE=B′D,∠EFB=60°,则线段DE的长是( )
如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若矩形的面积为16$\sqrt{3}$,AE=B′D,∠EFB=60°,则线段DE的长是( )| A. | 4$\sqrt{3}$ | B. | 5 | C. | 6 | D. | 6$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
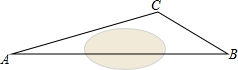 在一次课外实践活动中,同学们要测量某公园人工湖两侧A,B两个凉亭之间的距离.如图,现测得∠ABC=30°,∠CAB=15°,AC=200米,请计算A,B两个凉亭之间的距离(结果精确到1米)(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
在一次课外实践活动中,同学们要测量某公园人工湖两侧A,B两个凉亭之间的距离.如图,现测得∠ABC=30°,∠CAB=15°,AC=200米,请计算A,B两个凉亭之间的距离(结果精确到1米)(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com