
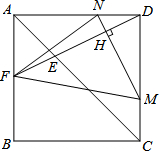
 ��ͼ��������ABCD�У�AB=a����λ��cm������E��M�ֱ����߶�AC��CD�ϵĶ��㣬����DE���ӳ��������εı��ڵ�F������M��MN��DF��H����AD��N����M�ӵ�C��������1cm/s���ٶ���CD���D�˶�����E�ӵ�A��������$\sqrt{2}$cm/s�ٶ���AC���C�˶����˶�ʱ��Ϊt��t��0���������ж���ȷ���ǣ�������
��ͼ��������ABCD�У�AB=a����λ��cm������E��M�ֱ����߶�AC��CD�ϵĶ��㣬����DE���ӳ��������εı��ڵ�F������M��MN��DF��H����AD��N����M�ӵ�C��������1cm/s���ٶ���CD���D�˶�����E�ӵ�A��������$\sqrt{2}$cm/s�ٶ���AC���C�˶����˶�ʱ��Ϊt��t��0���������ж���ȷ���ǣ�������| A�� | �٢ڢ� | B�� | �٢� | C�� | �٢ڢ� | D�� | �٢ڢۢ� |
���� ��֤����ADF�ա�DNC�����ɵõ�DF=MN��
������֤����AFE�ס�CDE�����ñ���ʽ���ʱ��t=$\frac{1}{3}$a�������õ�CM=$\frac{1}{3}$a=$\frac{1}{3}$CD��
���ɡ�AFE�ס�CDE���б���ʽ$\frac{AF}{CD}=\frac{AE}{EC}$=$\frac{1}{m}$���õ�a=mt+t������$\frac{CM}{CD}=\frac{t}{a}=\frac{t}{mt+t}=\frac{1}{m+1}$��
������MNFΪ���������Σ���������������Σ���Ҫ�������ۣ�
��� �⣺�ٵ�M������E�˶�ʱ��M��C�غϣ���ͼ1��
�ߡ�DNC+��ADF=90�㣬��DNC+��DCN=90�㣬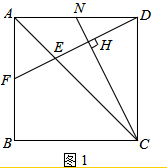
���ADF=��DCN��
�ڡ�ADF���DNC�У�
$\left\{\begin{array}{l}{��DAF=��CDN=90��}\\{AD=CD}\\{��ADF=��DCN}\end{array}\right.$��
���ADF�ա�DNC��ASA����
��DF=MN��
��ѡ�����ȷ��
����ͼ2������F�DZ�AB�е�ʱ����AF=$\frac{1}{2}$AB=$\frac{1}{2}$CD
��AB��CD�����AFE�ס�CDE��
��$\frac{AE}{EC}=\frac{AF}{CD}$=$\frac{1}{2}$��
��AE=$\frac{1}{2}$EC����AE=$\frac{1}{3}$AC=$\frac{\sqrt{2}}{3}$a��
��t=$\frac{AE}{\sqrt{2}}$=$\frac{1}{3}$a��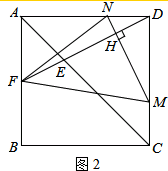
��CM=1•t=$\frac{1}{3}$a=$\frac{1}{3}$CD��
���MΪ��CD�����ȷֵ㣮
��ѡ�����ȷ��
�ۡߡ�AFE�ס�CDE
��$\frac{AF}{CD}=\frac{AE}{EC}$=$\frac{1}{m}$��
��$\frac{\sqrt{2}t}{\sqrt{2}a-\sqrt{2}t}=\frac{1}{m}$
��ã�a=mt+t��
��$\frac{CM}{CD}=\frac{t}{a}=\frac{t}{mt+t}=\frac{1}{m+1}$
��ѡ�����ȷ��
�ܡߡ�AFE�ס�CDE��
��$\frac{AF}{CD}=\frac{AE}{EC}$����$\frac{AF}{a}=\frac{\sqrt{2}t}{\sqrt{2}a-\sqrt{2}t}$����AF=$\frac{at}{a-t}$��
��֤��MND�ס�DFA��
��$\frac{ND}{AF}=\frac{DM}{AD}$����$\frac{ND}{\frac{at}{a-t}}=\frac{a-t}{a}$����ND=t��
��ND=CM=t��AN=DM=a-t��
����MNF�������������������������
��I����FN=MN������AN=DM֪��FAN�ա�NDM��
��AF=ND���� AF=$\frac{at}{a-t}$=t����t=0���������⣮
��������β����ڣ�
��II����FN=FM����MN��DF֪��HN=HM����DN=DM=MC��
��t=$\frac{1}{2}$a����ʱ��F���B�غϣ�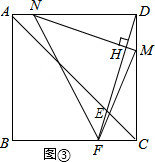
��III����FM=MN����Ȼ��ʱ��F��BC���ϣ���ͼ����ʾ��
��AN=DM��AD=CD��
��ND=CM��
��$\left\{\begin{array}{l}{ND=CM}\\{FM=MN}\end{array}\right.$��
���MFC�ա�NMD����FC=DM=a-t��
���ɡ�NDM�ס�DCF��
��$\frac{DN}{DM}=\frac{DC}{FC}$���� $\frac{t}{a-t}=\frac{a}{FC}$����FC=$\frac{a��a-t��}{t}$��
��$\frac{a��a-t��}{t}$=a-t��
��t=a����ʱ��F���C�غϣ�
������������t=a��t=$\frac{1}{2}$aʱ����MNF�ܹ���Ϊ����������
��ѡ�����ȷ��
���Ԣ٢ڢۢܶ���ȷ��
��ѡ��D��
���� �������˶��ͼ����ۺ��⣬���������������Ρ�ȫ�������Ρ������Ρ����������Ρ�����֤����֪ʶ�㣮����Ҫ���ǣ���1����ȷ������˶����̣���2����ȷ�˶������У�������߶Ρ�������֮��Ĺ�ϵ����3�����÷������۵���ѧ˼�룬����©�⣮


 �ظ���ʦ�㲦ϵ�д�
�ظ���ʦ�㲦ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
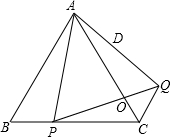 ��ͼ����֪�ȱߡ�ABC�ı߳�Ϊa����P��BC����һ���㣬��APΪ�����ȱߡ�APQ����PQ��AC�ڵ�O������CQ��
��ͼ����֪�ȱߡ�ABC�ı߳�Ϊa����P��BC����һ���㣬��APΪ�����ȱߡ�APQ����PQ��AC�ڵ�O������CQ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
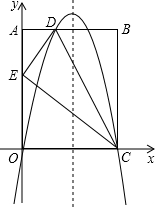 ��ͼ����ƽ��ֱ������ϵ�У���֪����OABC����������A��0��10����B��8��10����C��8��0������O��C�����������y=ax2+bx+c���߶�AB���ڵ�D����ֱ��CD�۵�����OABC��һ��BC��ʹ��B����OA���ϵĵ�E����
��ͼ����ƽ��ֱ������ϵ�У���֪����OABC����������A��0��10����B��8��10����C��8��0������O��C�����������y=ax2+bx+c���߶�AB���ڵ�D����ֱ��CD�۵�����OABC��һ��BC��ʹ��B����OA���ϵĵ�E�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
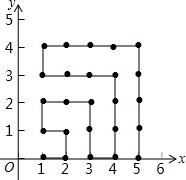 ��ͼ����ƽ��ֱ������ϵ�У������ɸ�������ֱ�Ϊ�����ĵ㣬��˳��ͼ�С������������У��磨1��0������2��0������2��1������1��1������1��2������2��2������������ɣ���2014���������Ϊ��45��11����
��ͼ����ƽ��ֱ������ϵ�У������ɸ�������ֱ�Ϊ�����ĵ㣬��˳��ͼ�С������������У��磨1��0������2��0������2��1������1��1������1��2������2��2������������ɣ���2014���������Ϊ��45��11�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a��b��c | B�� | a��c��b | C�� | b��c��a | D�� | c��b��a |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com