
”¾ĢāÄæ”æij³¬ŹŠ“ŁĻś»ī¶Æ£¬½«A£¬B£¬CČżÖÖĖ®¹ū²ÉÓĆ¼×”¢ŅŅ”¢±ūČżÖÖ·½Ź½“īÅä×°½ųĄńŗŠ½ųŠŠĻśŹŪ£®ĆæŗŠµÄ×ܳɱ¾ĪŖŗŠÖŠA£¬B£¬CČżÖÖĖ®¹ū³É±¾Ö®ŗĶ£¬ŗŠ×ӳɱ¾ŗöĀŌ²»¼Ę£®¼×ÖÖ·½Ź½ĆæŗŠ·Ö±š×°A£¬B£¬CČżÖÖĖ®¹ū6kg£¬3kg£¬1kg£»ŅŅÖÖ·½Ź½ĆæŗŠ·Ö±š×°A£¬B£¬CČżÖÖĖ®¹ū2kg£¬6kg£¬2kg£®¼×ĆæŗŠµÄ×ܳɱ¾ŹĒĆæĒ§æĖAĖ®¹ū³É±¾µÄ12.5±¶£¬ĆæŗŠ¼×µÄĻśŹŪĄūČóĀŹĪŖ20%£»ĆæŗŠ¼×±ČĆæŗŠŅŅµÄŹŪ¼ŪµĶ25%£»ĆæŗŠ±ūŌŚ³É±¾ÉĻĢįøß40%±ź¼Ūŗó“ņ°ĖÕŪ³öŹŪ£¬»ńĄūĪŖĆæĒ§æĖAĖ®¹ū³É±¾µÄ1.2±¶£®µ±ĻśŹŪ¼×”¢ŅŅ”¢±ūČżÖÖ·½Ź½“īÅäµÄĄńŗŠŹżĮæÖ®±ČĪŖ2£ŗ2£ŗ5Ź±£¬ŌņĻśŹŪ×ÜĄūČóĀŹĪŖ_____£®£ØĄūČóĀŹ£½ĄūČó”Ā³É±¾”Į100%£©
”¾“š°ø”æ20%
”¾½āĪö”æ
·Ö±šÉčĆæĒ§æĖA”¢B”¢CČżÖÖĖ®¹ūµÄ³É±¾ĪŖx”¢y”¢z£¬Éč±ūĆæŗŠ³É±¾ĪŖm£¬Č»ŗóøł¾ŻĢāŅā½«¼×”¢ŅŅ”¢±ūČżÖÖ·½Ź½µÄĆæŗŠ³É±¾ŗĶĄūČóÓĆx±ķŹ¾³öĄ“¼“æÉĒó½ā£®
ÉčĆæĒ§æĖA”¢B”¢CČżÖÖĖ®¹ūµÄ³É±¾·Ö±šĪŖĪŖx”¢y”¢z£¬ŅĄĢāŅāµĆ£ŗ
![]() £¬
£¬
”ą![]() £¬
£¬
”ąĆæŗŠ¼×µÄĻśŹŪĄūČó![]()
ŅŅÖÖ·½Ź½ĆæŗŠ³É±¾![]() £¬
£¬
ŅŅÖÖ·½Ź½ĆæŗŠŹŪ¼Ū![]() £¬
£¬
”ąĆæŗŠŅŅµÄĻśŹŪĄūČó![]() £¬
£¬
Éč±ūĆæŗŠ³É±¾ĪŖ![]() £¬ŅĄĢāŅāµĆ£ŗ
£¬ŅĄĢāŅāµĆ£ŗ![]() £¬
£¬
½āµĆ£ŗ![]() £®
£®
”ąµ±ĻśŹŪ¼×”¢ŅŅ”¢±ūČżÖÖ·½Ź½µÄĖ®¹ūŹżĮæÖ®±ČĪŖ2£ŗ2£ŗ5Ź±£¬
×ܳɱ¾ĪŖ£ŗ![]() £¬
£¬
×ÜĄūČóĪŖ£ŗ![]() £¬
£¬
ĻśŹŪµÄ×ÜĄūČóĀŹĪŖ£ŗ![]() ”Į100%£½20%£¬
”Į100%£½20%£¬
¹Ź“š°øĪŖ£ŗ20%£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£ŗÅ×ĪļĻßy£½x2+bx+cÓėÖ±Ļßy£½©x©1½»ÓŚµćA£¬B£®ĘäÖŠµćBµÄŗį×ų±źĪŖ2£®µćP£Øm£¬n£©ŹĒĻ߶ĪABÉĻµÄ¶Æµć£®
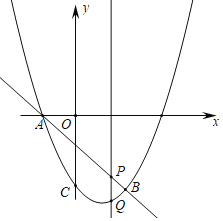
£Ø1£©ĒóÅ×ĪļĻߵıķ“ļŹ½£»
£Ø2£©¹żµćPµÄÖ±Ļß“¹Ö±ÓŚxÖį£¬½»Å×ĪļĻßÓŚµćQ£¬ĒóĻ߶ĪPQµÄ³¤¶ČlÓėmµÄ¹ŲĻµŹ½£¬mĪŖŗĪÖµŹ±£¬PQ×ī³¤£æ
£Ø3£©ŌŚĘ½½ĒÖ±½Ē×ų±źĻµÖŠ£¬ĪŅĆĒ°Ńŗį”¢×Ż×ų±ź¶¼ĪŖÕūŹżµÄµć³ĘĪŖÕūµć£¬¼Ē¶„µć¶¼ŹĒÕūµćµÄĖıߊĪĪŖÕūµćĖıߊĪ£¬ŌŚ£Ø2£©µÄĒéæöĻĀ£¬ŌŚĘ½ĆęÄŚÕŅ³öĖłÓŠ·ūŗĻŅŖĒóµÄÕūµćR£¬Ź¹P”¢Q”¢B”¢RĪŖÕūµćĘ½ŠŠĖıߊĪ£¬ĒėÖ±½ÓŠ“³öÕūµćRµÄ×ų±ź£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
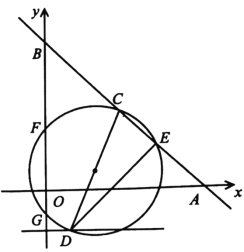
”¾ĢāÄæ”æČēĶ¼Ö±Ļß![]() ÓėxÖį”¢yÖį·Ö±š½»ÓŚµćA£¬B£¬CŹĒ
ÓėxÖį”¢yÖį·Ö±š½»ÓŚµćA£¬B£¬CŹĒ![]() µÄÖŠµć£¬µćDŌŚÖ±Ļß
µÄÖŠµć£¬µćDŌŚÖ±Ļß![]() ÉĻ£¬ŅŌ
ÉĻ£¬ŅŌ![]() ĪŖÖ±¾¶µÄŌ²ÓėÖ±Ļß
ĪŖÖ±¾¶µÄŌ²ÓėÖ±Ļß![]() µÄĮķŅ»½»µćĪŖE£¬½»yÖįÓŚµćF£¬G£¬ŅŃÖŖ
µÄĮķŅ»½»µćĪŖE£¬½»yÖįÓŚµćF£¬G£¬ŅŃÖŖ![]() £¬
£¬![]() £¬Ōņ
£¬Ōņ![]() µÄ³¤ŹĒ______£®
µÄ³¤ŹĒ______£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌĶĮĻĀĮŠ²ÄĮĻ£¬²¢Ķź³ÉĻąÓ¦µÄČĪĪń£®
¹ÅĻ£Ą°µÄ¼øŗĪѧ¼Ņŗ£Ā×ŌŚĖūµÄÖų×÷”¶¶ČĮæĀŪ”·Ņ»ŹéÖŠøų³öĮĖĄūÓĆČż½ĒŠĪČż±ßÖ®³¤ĒóĆ껿µÄ¹«Ź½©©©©ŗ£Ā×¹«Ź½S£½![]() £ØĘäÖŠa£¬b£¬cŹĒČż½ĒŠĪµÄČż±ß³¤£¬
£ØĘäÖŠa£¬b£¬cŹĒČż½ĒŠĪµÄČż±ß³¤£¬![]() £¬SĪŖČż½ĒŠĪµÄĆ껿£©£¬²¢øų³öĮĖÖ¤Ć÷
£¬SĪŖČż½ĒŠĪµÄĆ껿£©£¬²¢øų³öĮĖÖ¤Ć÷
ĄżČē£ŗŌŚ”÷ABCÖŠ£¬a£½3£¬b£½4£¬c£½5£¬ÄĒĆ“ĖüµÄĆ껿æÉŅŌÕāŃł¼ĘĖć£ŗ
”ßa£½3£¬b£½4£¬c£½5
”ą![]() £½6
£½6
”ąS£½![]() £½
£½![]() £½6
£½6
ŹĀŹµÉĻ£¬¶ŌÓŚŅŃÖŖČż½ĒŠĪµÄČż±ß³¤ĒóČż½ĒŠĪĆ껿µÄĪŹĢā£¬»¹æÉÓĆĪŅ¹śÄĻĖĪŹ±ĘŚŹżŃ§¼ŅĒŲ¾ÅÉŲĢį³öµÄĒŲ¾ÅÉŲ¹«Ź½µČ·½·Ø½ā¾ö£®
øł¾ŻÉĻŹö²ÄĮĻ£¬½ā“šĻĀĮŠĪŹĢā£ŗ
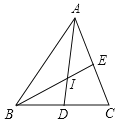
ČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬BC£½7£¬AC£½8£¬AB£½9
£Ø1£©ÓĆŗ£Ā×¹«Ź½Ēó”÷ABCµÄĆ껿£»
£Ø2£©ČēĶ¼£¬AD”¢BEĪŖ”÷ABCµÄĮ½Ģõ½ĒĘ½·ÖĻߣ¬ĖüĆĒµÄ½»µćĪŖI£¬Ēó”÷ABIµÄĆ껿£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚĘ½ĆęÖ±½Ē×ų±źĻµxOyÖŠ£¬Å×ĪļĻßy=mx2£2mx£3 (m”Ł0)ÓėyÖį½»ÓŚµćA£¬Ęä¶Ō³ĘÖįÓėxÖį½»ÓŚµćB£¬¶„µćĪŖCµć£®
£Ø1£©ĒóµćAŗĶµćBµÄ×ų±ź£»
£Ø2£©Čō”ĻACB£½45”ć£¬Ēó“ĖÅ×ĪļĻߵıķ“ļŹ½£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijĘóŅµĪŖĻģÓ¦¹ś¼Ņ½ĢÓż·öʶµÄŗÅÕŁ£¬¾ö¶Ø¶ŌijĻēÕņČ«ĢåʶĄ§³õ”¢øß֊ѧɜ½ųŠŠ×ŹÖś£¬³õ֊ѧɜĆæŌĀ׏֜200ŌŖ£¬øß֊ѧɜĆæŌĀ׏֜300ŌŖ£®ŅŃÖŖøĆĻēŹÜ׏֜µÄ³õ֊ѧɜČĖŹżŹĒŹÜ׏֜µÄøß֊ѧɜČĖŹżµÄ2±¶£¬ĒŅøĆĘóŅµŌŚ2018ÄźĻĀ°ėÄź7©12ŌĀÕā6øöŌĀ׏֜ѧɜ¹²Ö§³ö10.5ĶņŌŖ£®
£Ø1£©ĪŹøĆĻēÕņ·Ö±šÓŠ¶ąÉŁĆū³õ֊ѧɜŗĶøß֊ѧɜ»ńµĆĮĖ׏֜£æ
£Ø2£©2018Äź7©12ŌĀĘŚ¼ä£¬ŹÜ׏֜µÄ³õ”¢øß֊ѧɜ֊£¬·Ö±šÓŠ30%ŗĶ40%µÄѧɜ±»ĘĄĪŖÓÅŠćѧɜ£¬“Ó¶ų»ńµĆĮĖøĆĻēÕņÕžø®µÄ¹«æŖ±ķŃļ£®Ķ¬Ź±£¬Ģį¹©×ŹÖśµÄĘóŅµĪŖĮĖ¼¤·¢øü¶ąŹÜ׏֜ѧɜµÄ½ųČ”ŠÄŗĶѧĻ°ČČĒ飬¾ö¶Ø¶Ō2019ÄźÉĻ°ėÄź1©6ŌĀ±»ĘĄĪŖÓÅŠćѧɜµÄ³õ֊ѧɜĆæČĖĆæŌĀŌö¼Óa%µÄ׏֜£¬¶Ō±»ĘĄĪŖÓÅŠćѧɜµÄøß֊ѧɜĆæČĖĆæŌĀŌö¼Ó2a%µÄ׏֜£®ŌŚ“Ė½±ĄųÕž²ßµÄ¹ÄĄųĻĀ£¬2019Äź1©6ŌĀ±»ĘĄĪŖÓÅŠćѧɜµÄ³õ”¢øß֊ѧɜ·Öe±Č2018Äź7©12ŌĀµÄČĖŹżŌö¼ÓĮĖ3a%”¢a%£®ÕāŃł£¬2019ÄźÉĻ°ėğʥĪŖÓÅŠćѧɜµÄ³õ”¢øß֊ѧɜĖł»ńµĆµÄ׏֜×ܽš¶īŅ»øöŌĀ¾Ķ“ļµ½ĮĖ10800ŌŖ£¬ĒóaµÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
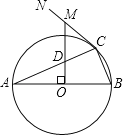
”¾ĢāÄæ”æČēĶ¼£¬ABŹĒ”ŃOµÄÖ±¾¶£¬µćCĪŖ”ŃOÉĻŅ»µć£¬CNĪŖ”ŃOµÄĒŠĻߣ¬OM”ĶABÓŚµćO£¬·Ö±š½»AC”¢CNÓŚD”¢MĮ½µć£®
£Ø1£©ĒóÖ¤£ŗMD=MC£»
£Ø2£©Čō”ŃOµÄ°ė¾¶ĪŖ5£¬AC=4![]() £¬ĒóMCµÄ³¤£®
£¬ĒóMCµÄ³¤£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
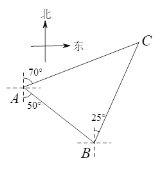
”¾ĢāÄæ”æČēĶ¼£¬ĀÖ“¬ŌŚA“¦¹Ū²āµĘĖžCĪ»ÓŚ±±Ę«¶«70o·½ĻņÉĻ£¬ĀÖ“¬“ÓA“¦ŅŌĆ抔Ź±30ŗ£ĄļµÄĖŁ¶ČŃŲÄĻĘ«¶«50o·½ĻņŌČĖŁŗ½ŠŠ£¬1Š”Ź±ŗ󵽓ļĀėĶ·B“¦£¬“ĖŹ±¹Ū²āµĘĖžCĪ»ÓŚ±±Ę«¶«25o·½ĻņÉĻ£¬ĒóµĘĖžCÓėĀėĶ·BÖ®¼äµÄ¾ąĄė(½į¹ū±£ĮōøłŗÅ).
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijŃųÖ³³”¼Ę»®ÓĆ96Ć×µÄÖńĄé°ŹĪ§³ÉČēĶ¼ĖłŹ¾µÄ¢Ł”¢¢Ś”¢¢ŪČżøöŃųÖ³ĒųÓņ£¬ĘäÖŠĒųÓņ¢ŁŹĒÕż·½ŠĪ£¬ĒųÓņ¢ŚŗĶ¢ŪŹĒ¾ŲŠĪ£¬ĒŅAG”ĆBG£½3”Ć2£®ÉčBGµÄ³¤ĪŖ2xĆ×£®
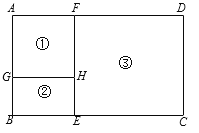
£Ø1£©ÓĆŗ¬xµÄ“śŹżŹ½±ķŹ¾DF£½ £»
£Ø2£©xĪŖŗĪÖµŹ±£¬ĒųÓņ¢ŪµÄĆ껿ĪŖ180Ę½·½Ć×£»
£Ø3£©xĪŖŗĪÖµŹ±£¬ĒųÓņ¢ŪµÄĆ껿×ī“ó£æ×ī“óĆ껿ŹĒ¶ąÉŁ£æ
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com