
【题目】在一节数学课上,老师布置了一个任务:
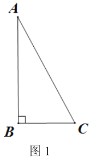
已知,如图1,在![]() 中,
中,![]() ,用尺规作图作矩形
,用尺规作图作矩形![]() .
.
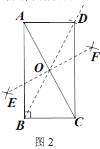
同学们开动脑筋,想出了很多办法,其中小亮作了图2,他向同学们分享了作法:
①分别以点![]() 、
、![]() 为圆心,大于
为圆心,大于![]() 长为半径画弧,两弧分别交于点
长为半径画弧,两弧分别交于点![]() 、
、![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ;
;
②作射线![]() ,在
,在![]() 上取点
上取点![]() ,使
,使![]() ;
;
③连接![]() ,
,![]() .
.
则四边形![]() 就是所求作的矩形.
就是所求作的矩形.
老师说:“小亮的作法正确.”
写出小亮的作图依据.
【答案】到线段两端距离相等的点在线段的垂直平分线上;直角三角形斜边上的中线等于斜边的一半;对角线互相平分且相等是矩形.
【解析】
根据到线段两端距离相等的点在线段的垂直平分线上可判断EF垂直平分AC,再根据直角三角形斜边上的中线等于斜边的一半得到BO=OA=OC,则由OD=OB得到BO=OA=OC=OD,从而根据矩形的判定方法可判断四边形ABCD就是所求作的矩形.
由作法得EF垂直平分AC,则OA=OC,
则BO为Rt△ABC斜边上的中线,
所以BO=OA=OC,
因为OD=OB,
所以BO=OA=OC=OD,
所以四边形ABCD为矩形.
所以小亮的作图依据为:到线段两端距离相等的点在线段的垂直平分线上;直角三角形斜边上的中线等于斜边的一半;对角线互相平分且相等是矩形.


科目:初中数学 来源: 题型:
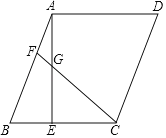
【题目】在ABCD中,AE⊥BC于点E,F为AB边上一点,连接CF,交AE于点G,CF=CB=AE.
(1)若AB![]() ,BC
,BC![]() ,求CE的长;
,求CE的长;
(2)求证:BE=CG﹣AG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知长方形ABCD的两个顶点A(2,-1),C(6,2)。点M为y轴上一点,△MAB的面积为6,且MD<MA。
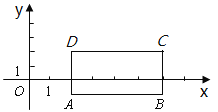
请解答下列问题:
(1)顶点B的坐标为 ;
(2)将长方形ABCD平移后得到![]() ,若
,若![]() ,则
,则![]() 的坐标为 ;
的坐标为 ;
(3)求点M的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
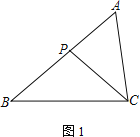
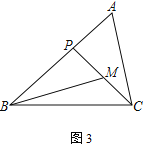
【题目】在△ABC中,P为边AB上一点.
(1) 如图1,若∠ACP=∠B,求证:AC2=AP·AB;
(2) 若M为CP的中点,AC=2,
① 如图2,若∠PBM=∠ACP,AB=3,求BP的长;
② 如图3,若∠ABC=45°,∠A=∠BMP=60°,直接写出BP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
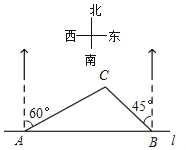
【题目】如图,在一条东西方向笔直的沿湖道路l上有A、B两个游船码头,观光岛屿C在码头A的北偏东60°方向、在码头B的北偏西45°方向,AC=4千米.那么码头A、B之间的距离等于_____千米.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
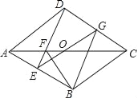
【题目】已知:如图,在菱形ABCD中,E是AB上一点,线段DE与菱形对角线AC交于点F,点O是AC的中点,EO的延长线交边DC于点G
(1)求证:∠AED=∠FBC;
(2)求证:四边形DEBG是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列解方程组的部分过程,回答下列问题
解方程组![]()
现有两位同学的解法如下:
解法一;由①,得x=2y+5,③
把③代入②,得3(2y+5)﹣2y=3.……
解法二:①﹣②,得﹣2x=2.……
(1)解法一使用的具体方法是________,解法二使用的具体方法是______,以上两种方法的共同点是________.
(2)请你任选一种解法,把完整的解题过程写出来
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某一蓄水池每1h的排水量V(m3/h)与排完水池中的水所用时间t(h)之间的函数图象。
(1)请你根据图象提供的信息求出此蓄水池的蓄水量;
(2)写出函数的函数表达式;
(3)若要6h排完水池的水,那么每1h的排水量应该是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的材料,回答问题:
解方程x4-5x2+4=0,这是一个一元四次方程,根据该方程的特点,它的解法通常是:
设x2=y,那么x4=y2,于是原方程可变为y2-5y+4=0 ①,解得y1=1,y2=4.
当y=1时,x2=1,∴x=±1;
当y=4时,x2=4,∴x=±2;
∴原方程有四个根:x1=1,x2=-1,x3=2,x4=-2.
在由原方程得到方程①的过程中,利用换元法达到降次的目的,体现了数学的转化思想,请利用上述方法解方程
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com