
分析 (1)根据题意举例即可,设循环四位数的千位数字与十位数字为m,百位数字与个位数字为n,分别表示出循环四位数和其对应数,再作差化简即可得;
(2)由(1)知,这个循环四位数与它的对应数的差为101×9(x-y),根据题意知x-y=4或x-y=8,即可得答案.
解答 解:(1)循环四位数为3434,其对应数为4343,
设循环四位数的千位数字与十位数字为m,百位数字与个位数字为n,
则循环四位数为1000m+100n+10m+n,其对应数为1000n+100m+10n+m,
“循环四位数”与它的“对应数”的差为(1000m+100n+10m+n)-(1000n+100m+10n+m)=101×9(m-n),
∴任意一个“循环四位数”与它的“对应数”的差都能被101整除;
(2)由(1)知,这个循环四位数与它的对应数的差为101×9(x-y),
∵这个循环四位数与它的对应数的差能被404整除,
∴x-y=4或x-y=8,
即y=x-4或y=x-8.
点评 本题主要考查因式分解的应用和列代数式及整式的化简,理解题意表示出循环四位数和其对应数是解题的关键.


科目:初中数学 来源: 题型:解答题
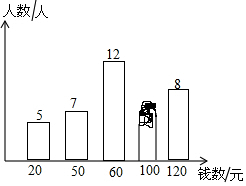 小明调查了学校50名同学本学期购买课外书的花费情况,并将结果绘制成了下面的统计图,由于不小心滴上了墨水,导致花费为100元的人数看不清楚了.求出这50名学生本学期购买课外书花费的众数、中位数和平均数.
小明调查了学校50名同学本学期购买课外书的花费情况,并将结果绘制成了下面的统计图,由于不小心滴上了墨水,导致花费为100元的人数看不清楚了.求出这50名学生本学期购买课外书花费的众数、中位数和平均数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
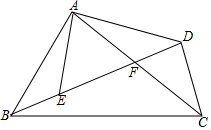 如图,在四边形ABCD中,AC、BD相交于点F,点E在BD上,且$\frac{AB}{AE}$=$\frac{BC}{ED}$=$\frac{AC}{AD}$.
如图,在四边形ABCD中,AC、BD相交于点F,点E在BD上,且$\frac{AB}{AE}$=$\frac{BC}{ED}$=$\frac{AC}{AD}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
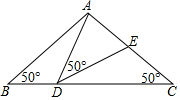 如图,在△ABC中,AB=AC=2,∠B=∠C=50°,点D在线段BC上运动(点D不与B、C重合),连接AD,作∠ADE=50°,DE交线段AC于E.
如图,在△ABC中,AB=AC=2,∠B=∠C=50°,点D在线段BC上运动(点D不与B、C重合),连接AD,作∠ADE=50°,DE交线段AC于E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com