
【题目】三角形角平分线交点或三角形内切圆的圆心都称为三角形的内心.按此说法,四边形的四个角平分线交于一点,我们也称为“四边形的内心”.
(1)试举出一个有内心的四边形.
(2)探究:对于任意四边形ABCD,如果有内心,则四边形的边长具备何种条件?为什么?
(3)探究:腰长为![]() 的等腰直角三角形ABC,∠C=90°,O是△ABC的内心,若沿图中虚线剪开,O仍然是四边形ABDE的内心,此时裁剪线有多少条?
的等腰直角三角形ABC,∠C=90°,O是△ABC的内心,若沿图中虚线剪开,O仍然是四边形ABDE的内心,此时裁剪线有多少条?
(4)问题(3)中,O是四边形ABDE内心,且四边形ABDE是等腰梯形,求DE的长?
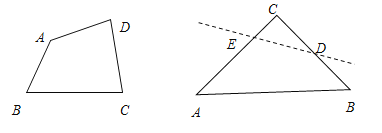
【答案】(1)正方形,菱形(写出一个即可) ;(2)对边之和相等;(3)有无数条 ;(4)![]() .
.
【解析】试题分析:(1)对角线平分每一对角的四边形都可以,如菱形、正方形;
(2)对于任意四边形ABCD,如果有内心,则四边形的边长具备条件是对边和相等;
(3)根据O到AB的距离等于O到DE的距离,即可得到答案;
(4)由勾股定理求出AB=2![]() ,过D作DF⊥AB于F,过E作EQ⊥AB于Q,得到平行四边形DEQF,推出DE=FQ,DF=EQ,根据等腰直角三角形得出AF=DF=BQ=QE,设DC=x,由勾股定理求出DE、AF、BQ的长,即AF+FQ+BQ=2
,过D作DF⊥AB于F,过E作EQ⊥AB于Q,得到平行四边形DEQF,推出DE=FQ,DF=EQ,根据等腰直角三角形得出AF=DF=BQ=QE,设DC=x,由勾股定理求出DE、AF、BQ的长,即AF+FQ+BQ=2![]() ,代入即可求出答案.
,代入即可求出答案.
试题解析:(1)答:一个有内心的四边形是菱形.
(2)答:对于任意四边形ABCD,如果有内心,则四边形的边长具备条件是对边和相等.
(3)解:有无数条,
理由是根据角平分线的性质得到:O到AB的距离等于O到DE的距离,在△ABC内有无数条,如图:具备DE∥AB即可.
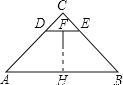
(4)解:等腰直角三角形ACB,AC=BC=2,由勾股定理得:AB=2![]() ,
,
过D作DF⊥AB于F,过E作EQ⊥AB于Q,


科目:初中数学 来源: 题型:
【题目】已知,四边形ABCD是正方形,点P在直线BC上,点G在直线AD上(P、G不与正方形顶点重合,且在CD的同侧),PD=PG,DF⊥PG于点H,交直线AB于点F,将线段PG绕点P逆时针旋转90°得到线段PE,连结EF.
(1)如图1,当点P与点G分别在线段BC与线段AD上时.
①求证:DG=2PC;
②求证:四边形PEFD是菱形;
(2)如图2,当点P与点G分别在线段BC与线段AD的延长线上时,请猜想四边形PEFD是怎样的特殊四边形,并证明你的猜想.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, ⊙O 的半径是2,直线l与⊙O 相交于A、B 两点,M、N 是⊙O 上的两个动点,且在直线l的异侧,若∠AMB=45°,则四边形MANB 面积的最大值是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
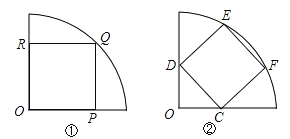
【题目】有一批圆心角为90o,半径为3的扇形下脚料,现利用这批材料截取尽可能大的正方形材料,如图有两种截取方法:
方法一:如图1所示,正方形OPQR的顶点P、Q、R均在扇形的边界上;
方法二:如图2所示,正方形顶点C、D、E、F均在扇形边界上.
试分别求这两种截取方法得到的正方形面积,并说明哪种截取方法得到的正方形面积更大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是边长为1的等边三角形,过点C的直线m平行AB,D、E分别是线段AB、直线m上的点,先按如图方式进行折叠,点A、C分别落在A′、C′处,且A′C′经过点B,DE为折痕,当C′E⊥m时,![]() 的值为_____.
的值为_____.
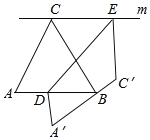
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小丽为了测旗杆AB的高度,小丽眼睛距地图1.5米,小丽站在C点,测出旗杆A的仰角为30o,小丽向前走了10米到达点E,此时的仰角为60o,求旗杆的高度。
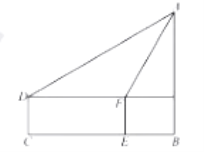
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在“数学小论文”评比活动中,共征集到论文100篇,对论文评比的分数(分数为整数)整理后,分组画出频数分布直方图(如图),已知从左到右5个小长方形的高的比为l:3:7:6:3,那么在这次评比中被评为优秀的论文(分数大于或等于80分为优秀)有____篇.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() ,
,![]() 之间有一条曲线和一条线段,
之间有一条曲线和一条线段,![]() 在线段
在线段![]() 上,己知
上,己知![]() ,
,![]() ,
,![]() 是线段
是线段![]() 上一动点,过点
上一动点,过点![]() 作
作![]() 交曲线于点
交曲线于点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() .设
.设![]() ,
,![]() 两点间的距离为
两点间的距离为![]() ,
,![]() ,
,![]() 两点间的距离为
两点间的距离为![]() .(当点
.(当点![]() 与点
与点![]() 重合时,
重合时,![]() 的值为
的值为![]() )小思根据学习函数的经验,对函数
)小思根据学习函数的经验,对函数![]() 随自变量
随自变量![]() 的变化而变化的规律进行了探究.
的变化而变化的规律进行了探究.
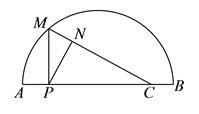
下面是小思的探究过程,请补充完整:
(![]() )通过取点,画图,测量,得到了
)通过取点,画图,测量,得到了![]() 与
与![]() 的几组值,补全下表:
的几组值,补全下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(说明:补全表格时相关数值保留一位小数)
(![]() )在下列平面直角坐标系中描出以补全后的表中各对对应值为坐标的点,画出该函数的图象.
)在下列平面直角坐标系中描出以补全后的表中各对对应值为坐标的点,画出该函数的图象.

(![]() )结合画出的函数图象,解决问题:当
)结合画出的函数图象,解决问题:当![]() 时,
时,![]() 的长度约为__________
的长度约为__________![]() (结果保留一位小数).
(结果保留一位小数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着越来越多年轻家长对低幼阶段孩子英语口语的重视,某APP顺势推出了“北美外教在线授课”系列课程,提供“A课程”、“B课程”两种不同课程供家长选择.已知购买“A课程”3课时与“B课程”5课时共需付款410元,购买“A课程”5课时与“B课程”3课时共需付款470元.
(1)请问购买“A课程”1课时多少元?购买“B课程”1课时多少元?
(2)根据市场调研,APP销售“A课程”1课时获利25元,销售“B课程”1课时获利20元,临近春节,小融计划用不低于3000元且不超过3600元的压岁钱购买两种课程共60课时,请问购买“A课程”多少课时才使得APP的获利最高?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com