
已知抛物线y=ax2+bx+c(a>0)经过点B(12,0)和C(0,-6),对称轴为x=2.
(1)求该抛物线的解析式.
(2)点D在线段AB上且AD=AC,若动点P从A出发沿线段AB以每秒1个单位长度的速度匀速运动,同时另一个动点Q以某一速度从C出发沿线段CB匀速运动,问是否存在某一时刻,使线段PQ被直线CD垂直平分?若![]() 存在,请求出此时的时间t(秒)和点Q的运动速度;若存在,请说明理由.
存在,请求出此时的时间t(秒)和点Q的运动速度;若存在,请说明理由.
 (3)在(2)的结论下,直线x=1上是否存在点M,使△MPQ为等腰三角形?若存在,请求出所有点M的坐
(3)在(2)的结论下,直线x=1上是否存在点M,使△MPQ为等腰三角形?若存在,请求出所有点M的坐
标;若存在,请说明理由.
解:∵抛物线 过C(6,0)
∴c=-6,即y=ax²+bx-6
由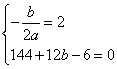 ,解得:a=
,解得:a=![]() ,b=-
,b=-![]()
∴抛物线解析式为y=![]() x²-
x²-![]() x-6
x-6
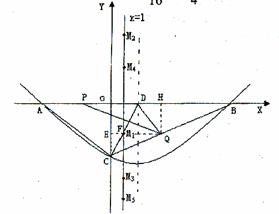
(2)存在,设直线DC垂直平分PQ
在Rt△AOC中,AC²8²+6²=100, ∴AC=10=AD
∴点D在对称轴上,连接DQ, 则∠PDC=∠QDC
∵∠PDC=∠ ACD
∴∠QDC=∠ ACD∴DQ∥AC,BD=AB-AD=10
DQ为△ABC的中位线,∴DQ=½AC=5
AP=AD-PD=AD-DQ=5
∴t=5/1=5秒
∴存在t=5秒时,直线DC垂直平分PQ
在Rt△BOC中,BC ² =6 ²+12 ²,BC=6![]() ,∴CQ=3
,∴CQ=3![]()
∴点Q的运动速度为3![]() /5秒/单位长度
/5秒/单位长度
(3)存在,过点Q作QH⊥x轴于H,QH=3,PH=9
在Rt△PQH中,PQ=![]() =3
=3![]()
①当MP=MQ时,设直线CD的解析式为:y=kx+b。k≠0
![]()
解得:![]() ,∴y=3x-6
,∴y=3x-6
当x=1时,y=-3 ∴m1(1,-3)
②当PQ为等腰三角形△MPQ的腰时,且p为顶点
设直线x=1上存在点M(1,y),有勾股定理得
4x²+y²=90,y=±![]()
∴M3(1, ![]() )M2(1, -
)M2(1, -![]() )
)
③当PQ为等腰三角形△MPQ的腰时,且Q为顶点
过点Q作QE⊥Y轴于E,交直线x=1于F,则F﹙1,-3﹚
设直线x=1上存在点M(1,y),有勾股定理得
(y+3)²+5²=90,y=-3±![]()
∴M4 (1, ![]() )M5 (1, -
)M5 (1, -![]() )
)
综上所述:存在这样的点:m1(1,-3) M3(1, ![]() )M2(1, -
)M2(1, -![]() ),M4 (1,
),M4 (1, ![]() )M5 (1, -
)M5 (1, -![]() )
)


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 (3)设点P为抛物线的对称轴x=1上的一动点,求使∠PCB=90°的点P的坐标.
(3)设点P为抛物线的对称轴x=1上的一动点,求使∠PCB=90°的点P的坐标.查看答案和解析>>
科目:初中数学 来源:2012届山东邹城北宿中学九年级3月月考数学试卷(带解析) 题型:解答题
已知抛物线y=ax2+bx-4a经过A(-1,0)、C(0,4)两点,与x轴交于另一点B.
(1)求抛物线的解析式;
(2)若点D(m,m+1)在第一象限的抛物线上, 求点D关于直线BC对称的点的坐标;
(3)在(2)的条件下,连结BD,若点P为抛物线上一点,且∠DBP=45°,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源:2010-2011年浙江省嵊州市九年级上学期期末考试数学卷 题型:解答题
(本小题满分14分)
如图,已知抛物线y=ax2+bx+c与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C(0,3)。设抛物线的顶点为D,求解下列问题:

1.(1)求抛物线的解析式和D点的坐标;
2.(2)过点D作DF∥ 轴,交直线BC于点F,求线段DF的长,并求△BCD的面积;
轴,交直线BC于点F,求线段DF的长,并求△BCD的面积;
3.(3)能否在抛物线上找到一点Q,使△BDQ为直角三角形?若能找到,试写出Q点的坐标;若不能,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com