
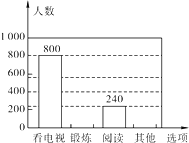
【题目】为了解某市市民晚饭后1小时内的生活方式,调查小组设计了“阅读”、“锻炼”、“看电视”和“其它”四个选项,用随机抽样的方法调查了该市部分市民,并根据调查结果绘制成如下统计图.
根据统计图所提供的信息,解答下列问题:
(1)本次共调查了________名市民;
(2)补全条形统计图;
(3)该市共有480万市民,估计该市市民晚饭后1小时内锻炼的人数.

【答案】(1)2000;(2)见解析;(3)该市共有480万市民,估计该市市民晚饭后1小时内锻炼的人数为96万.
【解析】
(1)根据“总人数=看电视人数÷看电视人数所占比例”即可算出本次共调查了多少名市民;
(2)根据“其它人数=总人数×其它人数所占比例”即可算出晚饭后选择其它的市民数,再用“锻炼人数=总人数-看电视人数-阅读人数-其它人数”即可算出晚饭后选择锻炼的人数,依此补充完整条形统计图即可;
(3)根据“本市选择锻炼人数=本市总人数×锻炼人数所占比例”即可得出结论.
(1)本次共调查的人数为:800÷40%=2000,
故答案为:2000.
(2)晚饭后选择其它的人数为:2000×28%=560,
晚饭后选择锻炼的人数为:2000-800-240-560=400.
将条形统计图补充完整,如图所示.
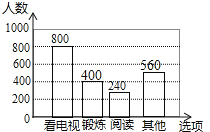
(3)晚饭后选择锻炼的人数所占的比例为:400÷2000=20%,
该市市民晚饭后1小时内锻炼的人数为:480×20%=96(万).
答:该市共有480万市民,估计该市市民晚饭后1小时内锻炼的人数为96万.


科目:初中数学 来源: 题型:
【题目】如图,已知点![]() ,动点
,动点![]() 从原点
从原点![]() 出发,沿
出发,沿![]() 轴正半轴运动,速度为每秒1个单位长度,以点
轴正半轴运动,速度为每秒1个单位长度,以点![]() 为直角顶点在第一象限内作等腰直角三角形
为直角顶点在第一象限内作等腰直角三角形![]() .设点
.设点![]() 的运动时间为
的运动时间为![]() 秒.
秒.
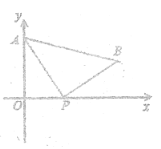
(1)若![]() 轴,求
轴,求![]() 的值;
的值;
(2)若![]() ,求点
,求点![]() 的坐标.
的坐标.
(3)当![]() 时,
时,![]() 轴上是否存在有一点
轴上是否存在有一点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 为顶点的三角形是等腰三角形,请直接写出点
为顶点的三角形是等腰三角形,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,抛物线y=ax2+2ax+c与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
(1)求抛物线的解析式;
(2)当a>0时,如图所示,若点D是第三象限方抛物线上的动点,设点D的横坐标为m,三角形ADC的面积为S,求出S与m的函数关系式,并直接写出自变量m的取值范围;请问当m为何值时,S有最大值?最大值是多少.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=15,点D是边BC上一动点(不与B、C重合),∠ADE=∠B=α,DE交AC于点E,且tanα=![]() 有以下的结论:① △ADE∽△ACD;② 当CD=9时,△ACD与△DBE全等;③ △BDE为直角三角形时,BD为12或
有以下的结论:① △ADE∽△ACD;② 当CD=9时,△ACD与△DBE全等;③ △BDE为直角三角形时,BD为12或![]() ;④ 0<BE≤
;④ 0<BE≤![]() ,其中正确的结论是___________(填入正确结论的序号)
,其中正确的结论是___________(填入正确结论的序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】牛奶是最古老的天然饮料之一,被誉为“白色血液”,对人体的重要性可想而知,现已成为国家营养餐计划备选食品之一.为推行国家营养餐计划,某乳品公司向某营养餐中心运输一批牛奶,由铁路运输每千克只需运费0.58 元;由公路运输,每千克需运费0.28元,还需其他费用600元.请探究选用哪种运输方式所需费用较少?
查看答案和解析>>
科目:初中数学 来源: 题型:
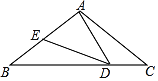
【题目】如图所示:在△ABC中,AB=AC=5,BC=8,D,E分别为BC.AB边上一点,∠ADE=∠C,
(1)求证:AD2=AEAB;
(2)∠ADC与∠BED是否相等?请说明理由;
(3)若CD=2,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l1:y=k1x+6与x轴、y轴分别交于A、B两点,且OB=![]() OA,直线l2:y=k2x+b经过点C(
OA,直线l2:y=k2x+b经过点C(![]() ,1),与x轴、y轴、直线AB分别交于点E、F、D三点.
,1),与x轴、y轴、直线AB分别交于点E、F、D三点.
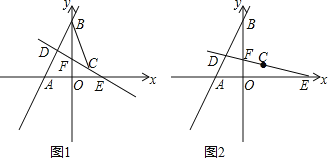
(1)求直线l1的解析式;
(2)如图1,连接CB,当CD⊥AB时,求点D的坐标和△BCD的面积;
(3)如图2,当点D在直线AB上运动时,在坐标轴上是否存在点Q,使△QCD是以CD为底边的等腰直角三角形?若存在,请直接写出点Q的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与x轴交于点A,与y轴交于点C.抛物线
与x轴交于点A,与y轴交于点C.抛物线![]() 经过A,C两点,且与x轴交于另一点B(点B在点A右侧).
经过A,C两点,且与x轴交于另一点B(点B在点A右侧).

(1)求抛物线的解析式及点B坐标;
(2)若点M是线段BC上的一动点,过点M的直线EF平行y轴交x轴于点F,交抛物线于点E.求ME长的最大值;
(3)试探究当ME取最大值时,在抛物线上、x轴下方是否存在点P,使以M,F,B,P为顶点的四边形是平行四边形?若存在,请求出点P的坐标;若不存在,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,△ ABC 在直角坐标系内,三个顶点的坐标分别为A(-2,2)、B(-1,0)、C(0,1)(正方形网格中每个小正方形的边长是一个单位长度).
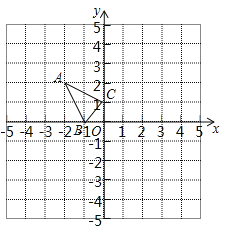
(1)画出△ ABC 关于 y 轴的轴对称图形△ A1B1C1;
(2)一点 O 为位拟中心,在网格内画出所有符合条件的△ A2B2C2,使△ A2B2C2 与△ A1B1C1 位拟,且位拟比为 2:1;
(3) △ A1B1C1 与△ A2B2C2 的面积比为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com