
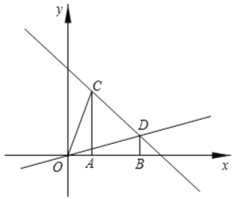
【题目】在平面直角坐标系中,过点C(1,3)、D(3,1)分别作x轴的垂线,垂足分别为A、B.
(1)求直线CD和直线OD的解析式;
(2)点M为直线OD上的一个动点,过M作x轴的垂线交直线CD于点N,是否存在这样的点M,使得以A、C、M、N为顶点的四边形为平行四边形?若存在,求此时点M的横坐标;若不存在,请说明理由;
(3)若△AOC沿CD方向平移(点C在线段CD上,且不与点D重合),在平移的过程中,设平移距离为![]() t,△AOC与△OBD重叠部分的面积记为s,试求s与t的函数关系式.
t,△AOC与△OBD重叠部分的面积记为s,试求s与t的函数关系式.
【答案】(1)直线OD的解析式为y=![]() x;(2)存在.满足条件的点M的横坐标
x;(2)存在.满足条件的点M的横坐标![]() 或
或![]() ,理由见解析;(3)S=﹣
,理由见解析;(3)S=﹣![]() (t﹣1)2+
(t﹣1)2+![]() .
.
【解析】
(1)理由待定系数法即可解决问题;
(2)如图,设M(m,![]() m),则N(m,-m+4).当AC=MN时,A、C、M、N为顶点的四边形为平行四边形,可得|-m+4-
m),则N(m,-m+4).当AC=MN时,A、C、M、N为顶点的四边形为平行四边形,可得|-m+4-![]() m|=3,解方程即可;
m|=3,解方程即可;
(3)如图,设平移中的三角形为△A′O′C′,点C′在线段CD上.设O′C′与x轴交于点E,与直线OD交于点P;设A′C′与x轴交于点F,与直线OD交于点Q.根据S=S△OFQ-S△OEP=![]() OFFQ-
OFFQ-![]() OEPG计算即可;
OEPG计算即可;
(1)设直线CD的解析式为y=kx+b,则有![]() ,解得
,解得![]() ,
,
∴直线CD的解析式为y=﹣x+4.
设直线OD的解析式为y=mx,则有3m=1,m=![]() ,
,
∴直线OD的解析式为y=![]() x.
x.
(2)存在.
理由:如图,设M(m,![]() m),则N(m,﹣m+4).
m),则N(m,﹣m+4).
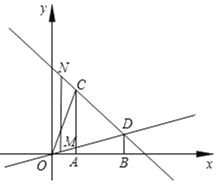
当AC=MN时,A、C、M、N为顶点的四边形为平行四边形,
∴|﹣m+4﹣![]() m|=3,
m|=3,
解得m=![]() 或
或![]() ,
,
∴满足条件的点M的横坐标![]() 或
或![]() .
.
(3)如图,设平移中的三角形为△A′O′C′,点C′在线段CD上.
设O′C′与x轴交于点E,与直线OD交于点P;
设A′C′与x轴交于点F,与直线OD交于点Q.
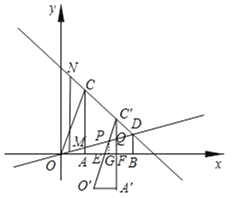
因为平移距离为![]() t,所以水平方向的平移距离为t(0≤t<2),
t,所以水平方向的平移距离为t(0≤t<2),
则图中AF=t,F(1+t,0),Q(1+t,![]() +
+![]() t),C′(1+t,3﹣t).
t),C′(1+t,3﹣t).
设直线O′C′的解析式为y=3x+b,
将C′(1+t,3﹣t)代入得:b=﹣4t,
∴直线O′C′的解析式为y=3x﹣4t.
∴E(![]() t,0).
t,0).
联立y=3x﹣4t与y=![]() x,解得x=
x,解得x=![]() t,
t,
∴P(![]() t,
t,![]() t).
t).
过点P作PG⊥x轴于点G,则PG=![]() t.
t.
∴S=S△OFQ﹣S△OEP=![]() OFFQ﹣
OFFQ﹣![]() OEPG
OEPG
=![]() (1+t)(
(1+t)(![]() +
+![]() t)﹣
t)﹣![]()
![]() t
t![]() t
t
=﹣![]() (t﹣1)2+
(t﹣1)2+![]() .
.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】(1)阅读下面材料:
点A、B在数轴上分别表示实数a、b, A、B两点之间的距离表示为AB,若a≥b,则 | a-b | = a-b;若a < b,则 | a-b | = b-a,当A、B两点中有一点在原点时, 不妨设点A在原,
如图甲, AB = OB =∣b∣=∣a b∣;当A、B两点都不在原点时,
![]()
① 如图乙,点A、B都在原点的右边,AB=OBOA=|b||a|=ba =|ab |;
![]()
②如图丙,点A、B都在原点的左边, AB = OB OA =|b||a|= b (a) = |ab|;
![]()
③如图丁,点A、B在原点的两边AB=OA+OB=|a|+|b|=a+(b) =|ab|.
![]()
综上所述,数轴上A、B两点之间的距离AB=∣ab∣.
(2)回答下列问题:
①数轴上表示1和3的两点之间的距离是______,数轴上表示1和3的两点之间的距离是______;
②数轴上表示x和1的两点分别是点A和B,则A、B之间的距离表示为______,如果AB=2,那么x =________ ;
③当代数式∣x +1∣+∣x 3∣取最小值时,相应的x的取值范围是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一边长为![]() 厘米的正方形纸板的四个角各剪去一个边长为
厘米的正方形纸板的四个角各剪去一个边长为![]() 厘米的小正方形,然后把它折成一个无盖纸盒.
厘米的小正方形,然后把它折成一个无盖纸盒.
(1)该纸盒的高是 厘米,底面积是 平方厘米;
(2)该纸盒的全面积(外表面积)为 平方厘米;
(3)为了使纸盒底面更加牢固且达到废物利用的目的,现考虑将剪下的四个小正方形平铺在盒子的底面,要求既不重叠又恰好铺满(不考虑纸板的厚度),求此时![]() 与
与![]() 之间的倍数关系.(直接写出答案即可)
之间的倍数关系.(直接写出答案即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2在第一象限内经过的整数点(横坐标、纵坐标都为整数的点)依次为A1,A2,A3…An,….将抛物线y=x2沿直线L:y=x向上平移,得一系列抛物线,且满足下列条件:①抛物线的顶点M1,M2,M3,…Mn,…都在直线L:y=x上;②抛物线依次经过点A1,A2,A3…An,….则顶点M2014的坐标为_______.
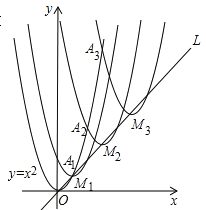
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】菱形ABCD中,∠BAD=60°,BD是对角线,点E、F分别是边AB、AD上两个点,且满足AE=DF,连接BF与DE相交于点G.
(1)如图1,求∠BGD的度数;
(2)如图2,作CH⊥BG于H点,求证:2GH=GB+DG;
(3)在满足(2)的条件下,且点H在菱形内部,若GB=6,CH=4![]() ,求菱形ABCD的面积.
,求菱形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线AC与BD交于点O,过点O作BD的垂线分别交AD,BC于E,F两点.若AC=2![]() ,∠DAO=30°,则FC的长度为( )
,∠DAO=30°,则FC的长度为( )
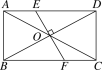
A. 1B. 2
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
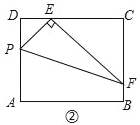
【题目】在矩形ABCD中,AD=3,CD=4,点E在CD上,且DE=1.
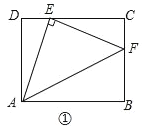
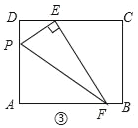
(1)感知:如图①,连接AE,过点E作EF丄AE,交BC于点F,连接AE,易证:△ADE≌△ECF(不需要证明);
(2)探究:如图②,点P在矩形ABCD的边AD上(点P不与点A、D重合),连接PE,过点E作EF⊥PE,交BC于点F,连接PF.求证:△PDE和△ECF相似;
(3)应用:如图③,若EF交AB于点F,EF丄PE,其他条件不变,且△PEF的面积是6,则AP的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y关于x的二次函数:y=![]() (m﹣n)x2+nx+t﹣n.
(m﹣n)x2+nx+t﹣n.
(1)当m=t=0时,判断该函数图象和x轴的交点个数;
(2)若n=t=3m,当x为何值时,函数有最值;
(3)是否存在实数m和t,使该函数图象和x轴有交点,且n的最大值和最小值分别为8和4?若存在,求m和t值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
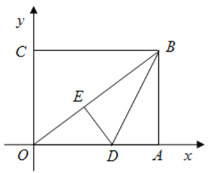
【题目】如图,在平面直角坐标系中,![]() 为坐标原点,矩形
为坐标原点,矩形![]() 的顶点
的顶点![]() 、
、![]() ,将矩形
,将矩形![]() 的一个角沿直线
的一个角沿直线![]() 折叠,使得点
折叠,使得点![]() 落在对角线
落在对角线![]() 上的点
上的点![]() 处,折痕与
处,折痕与![]() 轴交于点
轴交于点![]() .
.
(1)求线段![]() 的长度;
的长度;
(2)求直线![]() 所对应的函数表达式;
所对应的函数表达式;
(3)若点![]() 在线段
在线段![]() 上,在线段
上,在线段![]() 上是否存在点
上是否存在点![]() ,使以
,使以![]() 为顶点的四边形是平行四边形?若存在,请求出点
为顶点的四边形是平行四边形?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com