
某校为了了解本校九年级学生的视力情况(视力情况分为:不近视,轻度近视,中度近视,重度近视),随机对九年级的部分学生进行了抽样调查,将调查结果进行整理后,绘制了如下不完整的统计图,其中不近视与重度近视人数的和是中度近视人数的2倍.
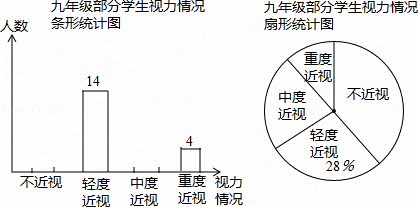
请你根据以上信息解答下列问题:
(1)求本次调查的学生人数;
(2)补全条形统计图,在扇形统计图中,“不近视”对应扇形的圆心角度数是 144 度;
(3)若该校九年级学生有1050人,请你估计该校九年级近视(包括轻度近视,中度近视,重度近视)的学生大约有多少人.
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
如图,以OA1=2为底边做等腰三角形,使得第三个顶点C1恰好在直线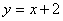 上,并以此向左、右依次类推,作一系列底边为2,第三个顶点在直线
上,并以此向左、右依次类推,作一系列底边为2,第三个顶点在直线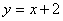 上的等腰三角形.
上的等腰三角形.
(1)底边为2,顶点在直线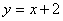 上且面积为21的等腰三角形位于图中什么位置?
上且面积为21的等腰三角形位于图中什么位置?
(2)求证:y轴右侧的每一个等腰三角形的面积都等于前后两个以腰为一边的三角形面积之和的
一半( 如:S右1=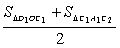 ,S右2
,S右2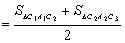 ).
).
(3)过D1、A1、C2三点画抛物线.问在抛物线上是否存在点P,使得△PD1C2的面积是△C1OD1与△C1A1C2面积和的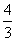 .若存在,请求出点P的坐标;若不存在,请说明理由.
.若存在,请求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
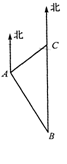
钓鱼岛及其附属岛屿是我国的固有领土,台湾保钓人士
组团前往钓鱼岛,宣示主权.当保钓船航行至海面B处时(如图),
测得钓鱼岛位于正北方向20海里的C处,为了防止日本海巡警干扰,
就请求我A处的海监船前往C处护航.已知C处位于A处的北偏东45°
的方向上, A位于B的北偏西30°的方向上.
求A、C之间的距离? (结果精确到0.1海里,参考数据: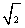 ≈1.41,
≈1.41,
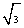 ≈1.73).
≈1.73).

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面直角坐标系中,点A(0,4),B(3,0),连接AB,将△AOB沿过点B的直线折叠,使点A落在x轴上的点A′处,折痕所在的直线交y轴正半轴于点C,则直线BC的解析式为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
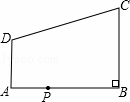
如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=8,AD=3,BC=4,点P为AB边上一动点,若△PAD与△PBC是相似三角形,则满足条件的点P的个数是( )
|
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:
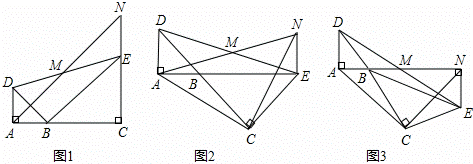
如图,已知△BAD和△BCE均为等腰直角三角形,∠BAD=∠BCE=90°,点M为DE的中点,过点E与AD平行的直线交射线AM于点N.
(1)当A,B,C三点在同一直线上时(如图1),求证:M为AN的中点;
(2)将图1中的△BCE绕点B旋转,当A,B,E三点在同一直线上时(如图2),求证:△ACN为等腰直角三角形;
(3)将图1中△BCE绕点B旋转到图3位置时,(2)中的结论是否仍成立?若成立,试证明之,若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
下图是数值转换机的示意图,小明按照其对应关系画出了y与x的函数图象.
(1)分别写出当0≤x≤4与x>4时,y与x的函数关系式;
(2)小明说:“所输出y的值为3时,输入x的值为0或5.”你认为他说的对吗?
试结合图象说明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com