
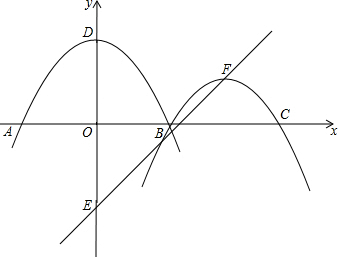
 如图:二次函数y=ax2+c(a<0,c>0)的图象C1交
如图:二次函数y=ax2+c(a<0,c>0)的图象C1交分析 (1)在y=ax2+c中令y=0,求x的值,可求得B点坐标;
(2)利用B、C的对称性,可求得C点坐标,利用两点式可求得C2的解析式;
(3)先求得点F坐标,过F作FG⊥y轴于,由条件可得GE=GF,从而可得到关于a、c的数量关系式.
解答 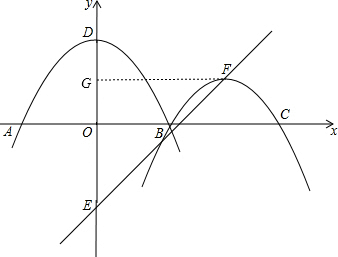 解:
解:
(1)y=ax2+c中令y=0,
可得ax2+c=0,解得x=±$\sqrt{-\frac{c}{a}}$,
∵B点在y轴的右侧,
∴B点坐标为($\sqrt{-\frac{c}{a}}$,0);
(2)∵点B、C关于直线x=$\frac{4}{3}$$\sqrt{-\frac{c}{a}}$上对称
∴C点坐标为($\frac{5}{3}\sqrt{-\frac{c}{a}}$,0),
∴抛物线的解析式为y=a(x-$\sqrt{-\frac{c}{a}}$)(x-$\frac{5}{3}\sqrt{-\frac{c}{a}}$);
(3)在y=a(x-$\sqrt{-\frac{c}{a}}$)(x-$\frac{5}{3}\sqrt{-\frac{c}{a}}$)中,
当x=$\frac{4}{3}$$\sqrt{-\frac{c}{a}}$时,可得y=$\frac{c}{9}$,
∵D、E关于x轴对称,
∴E点坐标为(0,-c),
∴OE=c,
∴GE=c+$\frac{c}{9}$,
过点F作FG⊥y轴于G,如图,则GF=$\frac{4}{3}$$\sqrt{-\frac{c}{a}}$,
∵∠DEF=45°,
∴GE=GF,
∴$\frac{4}{3}$$\sqrt{-\frac{c}{a}}$=c+$\frac{c}{9}$,整理可得ac=-$\frac{36}{25}$
点评 本题为二次函数综合应用,主要涉及二次函数的对称性、解析式、等腰直角三角形的性质等知识点.在(1)中利用函数与方程的关系是解题的关键,在(2)中利用对称性求得C点坐标是解题的关键,在(3)中利用45°角得到GE=GF是解题的关键.本题知识点不多,但计算量较大,综合性较强,难度适中.


 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:初中数学 来源: 题型:解答题
 如图,四边形ABCD是菱形,点E、F、G、H是AD、AB、BC、CD的中点.
如图,四边形ABCD是菱形,点E、F、G、H是AD、AB、BC、CD的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与点C重合,再展开,折痕EF交AD边于点E,交BC边于点F,分别连结AF和CE.
已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与点C重合,再展开,折痕EF交AD边于点E,交BC边于点F,分别连结AF和CE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com