练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    16．如图，在△ABC中，D是BC边上一点，且AB=AD=DC，∠C=35°，则∠BAD为（　　）
    A．25°B．35°C．40°D．50°

    分析 题中给出了相等的边，以及角的度数，再让求其它角的度数，这就需要利用“等边对等角”、“三角形的内角和是180°”，以及三角形的内角与外角的关系进行解答．

    解答 解：∵AD=DC，
    ∴∠DAC=∠C=35°，
    ∴∠ADB=∠DAC+∠C=70°．
    ∵AB=AD，
    ∴∠B=∠ADB=70°，
    ∴∠BAD=180°-∠B-∠ADB=180°-70°-70°=40°．
    故选：C．

    点评 本题考查了等腰三角形的性质及三角形内角和为180°等知识．此类已知三角形边之间的关系求角的度数的题，一般是利用等腰（等边）三角形的性质得出有关角的度数，进而求出所求角的度数．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

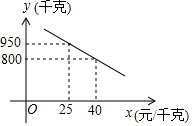    6．某商场经营一种海产品，进价是每千克20元，根据市场调查发现，每日的销售量y（千克）与售价x（元/千克）是一次函数关系，如图所示：
    （1）求y与x的函数关系式（不求自变量取值范围）；
    （2）某日该商场出售这种海产品获得了21000元的利润，该海产品的售价是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．解方程：$\frac{2}{x-4}$=2+$\frac{x+1}{4-x}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．已知a+b=4，2ab=3，求（a-b）2的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

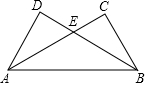    11．如图，AC=BD，AC⊥BC于C，BD⊥AD于D，AC与BD交于点E．有下列结论：①△ABC≌△BAD；②△ADE≌△BCE；③点E在线段AB的垂直平分线上．以上结论正确的有（　　）
    A．①B．②C．①和②D．①和②和③

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．在△ABC中，AB=AC，∠BAC=100°，将线段AC绕着点C逆时针旋转得到线段CD，旋转角为α，且0°＜α＜180°，连接AD、BD．
    （1）如图1，当α=60°时，∠CBD 的大小为30°；
    （2）当α=20°时，在图2的位置画出对应的图形；
    （3）若∠CBD=30°，请直接写出α的所有值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．如图，在8×8的方格纸中每个小正方形的边长均为l，线段AB的端点在小正方形的顶点上，（所画图形顶点必须在小正方形的顶点上）．
    （1）在图1中画一个以AB为边的四边形ABCD是中心对称图形，且四边形面积是12；
    （2）在图2中画一个以AB为边的四边形ABMN是轴对称图形，且只有一个角是直角，面积为15．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．如图，△ABC中，∠ACB=90°，BE平分∠ABC，ED⊥AB于点D，若AC=9cm，则AE+DE等于（　　）
    A．7cmB．8cmC．9cmD．10cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．计算
    （1）（-3）+（-5）
    （2）（+$\frac{1}{3}$）-（-$\frac{2}{3}$）+（-2）
    （3）（$\frac{2}{3}$-$\frac{1}{6}$+$\frac{5}{12}$）×（-24）
    （4）（-2）2÷（-$\frac{2}{3}$）+|-$\frac{1}{8}$|×（-2）3．

    查看答案和解析>>

    同步练习册答案