
【题目】如图,已知正方形ABCD的边长是2,E是DC上一点,△ADE经顺时针旋转后与△ABF重合.
(1)指出旋转的中心和旋转的角度;
(2)如果连结EF,那么△AEF是怎样的三角形?请说明理由.
(3)已知点G在BC上,且∠GAE=45°.
① 试说明GE=DE+BG.
② 若E是DC的中点,求BG的长.
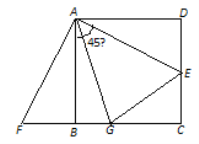
【答案】(1)旋转的中心是点A,旋转的角度是90°(2)△AEF是等腰直角三角形(3)①证明见解析② BG=![]()
【解析】试题分析:(1)根据正方形的性质得到AB=AD,∠BAD=90°,然后利用旋转的定义得到当△ADE经顺时针旋转后与△ABF重合时,可确定旋转的中心和旋转的角度;
(2)由(1)得到△ADE绕着点A逆时针旋转90°后与△ABF重合,根据旋转的性质得∠FAE=90°,AF=AE,由此可判断△AEF是等腰直角三角形;
(3)①首先得出AG是线段EF的垂直平分线,进而得出DE+GB=BF+BG=GF,即可得出答案;
②首先设GB=x,则GC=2-x,GE=1+x.在Rt△ECG中,∠C=90°,由勾股定理,得1+(2-x)2=(1+x)2,求出x即可.
试题解析:(1)∵四边形ABCD为正方形,
∴AB=AD,∠BAD=90°,
∴当△ADE经顺时针旋转后与△ABF重合时,旋转的中心是点A,旋转的角度是90°;
(2)△AEF是等腰三角形,理由:
∵四边形ABCD是正方形,
∴∠BAD=90°,
∴△ADE绕点A顺时针旋转90°后与△ABF重合,
∴△ADE≌△ABF,
∴AE=AF,
又∵∠EAF=90°,
∴△AEF是等腰三角形;
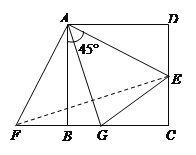
(3)①∵ ∠GAE=45°,∠EAF=90°,
∴ AG是∠EAF的平分线,
又∵ AF=AE,
∴ AG是线段EF的垂直平分线,
∴ GE=GF.
∵ DE=BF,
∴ DE+GB=BF+BG=GF,
∴ GE=DE+BG;
② ∵ E是DC的中点,
∴ DE=EC=FB=1,
设GB=x,则GC=2-x,GE=1+x,
在Rt△ECG中,∠C=90°,由勾股定理,得
1+(2-x)2=(1+x)2,
解这个方程,得x=![]() ,
,
即:BG=![]() .
.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:
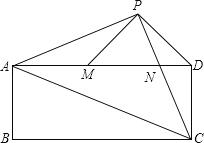
【题目】已知:如图,在矩形ABCD中,AC是对角线.点P为矩形外一点且满足AP=PC,AP⊥PC.PC交AD于点N,连接DP,过点P作PM⊥PD交AD于M.
(1)若AP=![]() ,AB=
,AB=![]() BC,求矩形ABCD的面积;
BC,求矩形ABCD的面积;
(2)若CD=PM,求证:AC=AP+PN.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OA⊥OB,等腰直角三角形CDE的腰CD在OB上,∠ECD=45°,将三角形CDE绕点C逆时针旋转75°,点E的对应点N恰好落在OA上,则![]() 的值为( )
的值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC.中,AB=BC,将△ABC绕点B顺时针旋转α度,得到△A1BC1,A1B交AC于点E,A1C1分别交AC、BC于点D、F,下列结论:①∠CDF=α,②A1E=CF,③DF=FC,④A1F=CE.其中正确的是 (写出正确结论的序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下问题,不适合用全面调查的是( )
A.了解全班同学每周体育锻炼的时间B.鞋厂检查生产的鞋底能承受的弯折次数
C.学校招聘教师,对应聘人员面试D.某中学调查全校753名学生的身高
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,D是边AC上一点,连接BD.将△BCD绕点B逆时针旋转60°得到△BAE,连接ED.若BC=10,BD=9,求△AED的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=30,∠AOB 内有一定点 P,且 OP=12,在 OA 上有一动点 Q,OB 上有 一动点 R。若△PQR 周长最小,则最小周长是( )
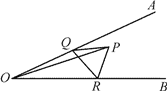
A. 6 B. 12 C. 16 D. 20
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com