

分析 (1)根据D组所对应的圆心角即可求得对应的比例,利用D组的人数除以对应的比例即可求得抽查的总人数,然后根据频率定义求解;
(2)利用总人数减去其它组的人数即可求得C组人数,补全直方图;
(3)利用总人数乘以对应的比例即可求解.
解答 解:(1)抽查的人数是42÷$\frac{84}{360}$=180(人),
选择景区A的学生的频率是:$\frac{36}{180}$=$\frac{1}{5}$.
故答案是:180,$\frac{1}{5}$;
(2)C组的人数是180-36-30-42=72(人),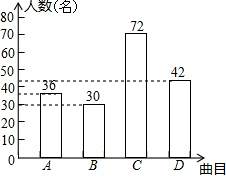 ;
;
(3)全校学生选择景区C的人数是120×$\frac{72}{180}$=480(人).
答:全校选择景区C的人数是480人.
点评 本题考查的是条形统计图的综合运用.读懂统计图,从统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 甲较为稳定 | B. | 乙较为稳定 | ||
| C. | 两个人成绩一样稳定 | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 有这样一个问题:如图,在四边形ABCD中,AB=AD,CB=CD,我们把这种两组邻边分别相等的四边形叫做筝形.请探究筝形的性质与判定方法.
有这样一个问题:如图,在四边形ABCD中,AB=AD,CB=CD,我们把这种两组邻边分别相等的四边形叫做筝形.请探究筝形的性质与判定方法.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com