Question

现计划把甲种货物1240吨和乙种货物880吨用一列货车运往某地，已知这列货车挂有A、B两种不同规格的货车厢共40节，使用A型车厢每节费用为0.6万元，使用B型车厢每节费用为0.8万元．

1.设运送这批货物的总费用为y万元，这列货车挂A型车厢x节，试写出y与x之间的函数关系式；

2.如果每节A型车厢最多可装甲种货物35吨和乙种货物15吨，每节B型车厢最多可装甲种货物25吨和乙种货物35吨，装货时按此要求安排A、B两种车厢的节数，那么共有哪几种安排车厢的方案？

3.在上述方案中，哪个方案运费最省？最少运费为多少元？

 

Answer 1

【答案】

 

1.设用A型车厢x节，则用B型车厢(40－x)节，总运费为y万元 ．-------1分

依题意，得  y＝0.6 x＋0.8(40－x)      --------------------------------3分

             ＝－0.2 x＋32    ----------------------------------------4分

2.依题意，得

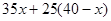≥1240，

≥880．       ---------------------------6分

化简，得   10 x≥240，     x≥24，  

            520≥20 x；      x≤26．

∴  24≤x≤26．                           --------------------------7分

∵  x取整数，故A型车厢可用24节或25节或26节．相应有三种装车方案：①24节A型车厢和16节B型车厢；②25节A型车厢和15节B型车厢；③26节A型车厢和14节B型车厢．     ----------------------------------------------------------8分

3.由函数y＝－0. 2 x＋32知，x越大，y越少，

故当x＝26时，运费最省．----------------------------------------------10分

这时 y＝－0.2×26＋32＝26.8(万元)                       --------------11分

答：安排A型车厢26节、B型车厢14节运费最省．最小运费为26.8万元．----12分　　  　　　　　                                      

（注：若直接算出三种方案的运费来比较，得出正确的最少运费亦给满分。）

【解析】（1）总费用=0.6×A型车厢节数+0.8×B型车厢节数．

（2）应分别表示出两类车厢能装载的甲乙两种货物的质量．35×A型车厢节数+25×B型车厢节数≥1240；15×A型车厢节数+35×B型车厢节数≥880．

（3）应结合（1）的函数，（2）的自变量的取值来解决