
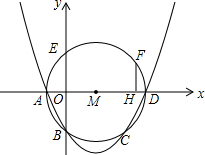
 ��ͼ����ƽ��ֱ������ϵ�У�������y=ax2+bx+c���M�ཻ��A��B��C��D�ĵ㣬����A��B���������ֱ�Ϊ��-1��0������0��-2������D��x������ADΪ��M��ֱ������E�ǡ�M��y�����һ�����㣬���ӻ�$\widehat{ED}$�ϵĵ�F��FH��AD�ڵ�H����FH=1.5
��ͼ����ƽ��ֱ������ϵ�У�������y=ax2+bx+c���M�ཻ��A��B��C��D�ĵ㣬����A��B���������ֱ�Ϊ��-1��0������0��-2������D��x������ADΪ��M��ֱ������E�ǡ�M��y�����һ�����㣬���ӻ�$\widehat{ED}$�ϵĵ�F��FH��AD�ڵ�H����FH=1.5���� ��1�����ȸ���Բ����Գ��������D�����꣬��A��B��D������룬�����������Ĵ𰸣�
��2�����ڵ�E���B ����x��Գƣ����ԣ�����BF��ֱ��BF��x��Ľ��㣬��Ϊ��P���ݴ˼��ɵý⣻
��3����CM=MQ��CM=CQ��MQ=CQ����������з������ݴ˼��ɵý⣮
��� �⣺��1������BD��
��AD�ǡ�M��ֱ�������ABD=90��
���AOB�ס�ABD��
��$\frac{AO}{AB}$=$\frac{AB}{AD}$��
��Rt��AOB��AO=1��BO=2��
���ݹ��ɶ����ã�AB=$\sqrt{5}$��
��$\frac{1}{\sqrt{5}}=\frac{\sqrt{5}}{AD}$��
��AD=5��
��DO=AD-AO=5-1=4��
��D��4��0����
�ѵ�A��-1��0����B��0��-2����D��4��0������y=ax2+bx+c�ɵã�
$\left\{\begin{array}{l}{c=-2}\\{16a+4b+c=0}\\{a-b+c=0}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{b=-\frac{3}{2}}\\{c=-2}\end{array}\right.$��
�������߱���ʽΪ��$y=\frac{1}{2}{x}^{2}-\frac{3}{2}x-2$��
��2������FM��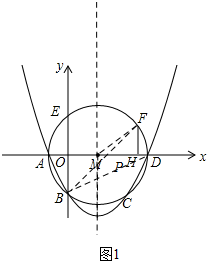
��Rt��FHM��FM=$\frac{5}{2}$��FH=$\frac{3}{2}$��
��MH=$\sqrt{��\frac{5}{2}��^{2}-��\frac{3}{2}��^{2}}$=2��
OM=AM-OA=$\frac{5}{2}$-1=$\frac{3}{2}$��
��OH=OM+MH=$\frac{3}{2}$+2=$\frac{7}{2}$��
��F��$\frac{7}{2}$��$\frac{3}{2}$����
��ֱ��BF�Ľ���ʽΪy=kx+b��
��$\left\{\begin{array}{l}{\frac{7}{2}k+b=\frac{3}{2}}\\{b=-2}\end{array}\right.$��
��ֱ��BF�Ľ���ʽΪ��y=x-2��
����BF��x���ڵ�P���ߵ�E���B����x��Գƣ�
���P������
��y=0ʱ��x=2��
��P��2��0����
��3����ͼ��CM=$\frac{5}{2}$
������$y=\frac{1}{2}{x}^{2}-\frac{3}{2}x-2$�ĶԳ���Ϊֱ��x=$\frac{3}{2}$��
��OM=$\frac{3}{2}$�����M��ֱ��x=$\frac{3}{2}$�ϣ�
����Բ�ĶԳ��Կ�֪����C���B����ֱ��x=$\frac{3}{2}$�Գƣ�
���C��3��-2����
�ٵ�CM=MQ=$\frac{5}{2}$ʱ����Q������x���Ϸ���Ҳ������x���·���
��Q1��$\frac{3}{2}$��$\frac{5}{2}$����Q2��$\frac{3}{2}$��$-\frac{5}{2}$����
�ڵ�CM=CQʱ������C��CN��MQ��
��MN=NQ=2����MQ=4��
��Q3��$\frac{3}{2}$��-4����
�۵�CQ4=MQ4ʱ������C��CR��MQ��Q4V��CM��
��MV=CV=$\frac{5}{4}$��Q4V=$\sqrt{M{{Q}_{4}}^{2}-\frac{25}{16}}$��
Rt��CRM��Rt��Q4VM��
��$\frac{M{Q}_{4}}{\frac{5}{2}}=\frac{\sqrt{M{{Q}_{4}}^{2}-\frac{25}{16}}}{\frac{3}{2}}$��
��ã�MQ4=$\frac{25}{16}$��
��Q4��$\frac{3}{2}$��-$\frac{25}{16}$��
���Ͽ�֪�������ĸ��㣬����
Q1��$\frac{3}{2}$��$\frac{5}{2}$����Q2��$\frac{3}{2}$��$-\frac{5}{2}$����Q3��$\frac{3}{2}$��-4����Q4��$\frac{3}{2}$��-$\frac{25}{16}$����
���� ������Ҫ�����˶��κ����������ߵĽ���ʽ�����Լ����ݶԳ����߶ε���Сֵ�����⣬�������˵��������ε�֪ʶ�����������ε�֪ʶ����һ���ۺ��Ժ�ǿ����Ŀ��ע�������ܽᣮ



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��һ�������� | B�� | ��һ�������� | C�� | �ڶ��������� | D�� | ������������ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
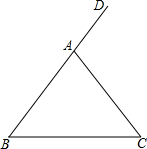 ��ͼ���ڡ�ABC�У�AB=AC����DAC�ǡ�ABC��һ����ǣ�
��ͼ���ڡ�ABC�У�AB=AC����DAC�ǡ�ABC��һ����ǣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ֱ֪��y=x+k��˫����y=$\frac{k+1}{x}$��kΪ������������A��B���㣮
��ͼ����ֱ֪��y=x+k��˫����y=$\frac{k+1}{x}$��kΪ������������A��B���㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
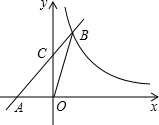 ��ͼ����ƽ��ֱ������ϵϵ�У�ֱ��y=k1x+2��x�ύ�ڵ�A����y�ύ�ڵ�C���뷴��������y=$\frac{{k}_{2}}{x}$�ڵ�һ�����ڵ�ͼ���ڵ�B������BO����S��OBC=1��tan��BOC=$\frac{1}{3}$����k2��ֵ�ǣ�������
��ͼ����ƽ��ֱ������ϵϵ�У�ֱ��y=k1x+2��x�ύ�ڵ�A����y�ύ�ڵ�C���뷴��������y=$\frac{{k}_{2}}{x}$�ڵ�һ�����ڵ�ͼ���ڵ�B������BO����S��OBC=1��tan��BOC=$\frac{1}{3}$����k2��ֵ�ǣ�������| A�� | -3 | B�� | 1 | C�� | 2 | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
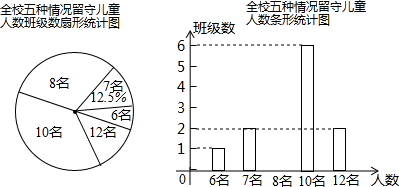
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
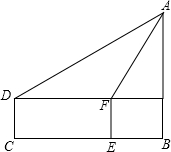 С��Ϊ�˲����AB�ĸ߶ȣ�С���۾������1.5�ף�С��վ��C�㣬������A������Ϊ30�㣬С����ǰ����10�����E����ʱ������Ϊ60�㣬����˵ĸ߶ȣ�
С��Ϊ�˲����AB�ĸ߶ȣ�С���۾������1.5�ף�С��վ��C�㣬������A������Ϊ30�㣬С����ǰ����10�����E����ʱ������Ϊ60�㣬����˵ĸ߶ȣ��鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com