
【题目】二次函数y=ax2+bx+c(a≠0)的图象所示,对称轴为x=1,给出下列结论:①abc>0;②当x>2时,y>0;③3a+c>0;④3a+b>0.其中正确的结论有( )

A. ①② B. ①④ C. ①③④ D. ②③④
【答案】C
【解析】
由二次函数图象开口方向、对称轴的位置、图象与y轴交点的位置得到a、b、c的符号,即可判①;由图象可知,当x=0时,y<0,根据对称轴为x=1可得当x=2时,y<0,观察图象即可判定②;由图象可知,x=-1时,y>0,即可得a-b+c=0,根据对称轴-![]() =1,可得b=-2a,代入即可判定③;由-
=1,可得b=-2a,代入即可判定③;由-![]() =1可得2a+b=0,所以3a+b=2a+b+a=a>0,即可判定④.
=1可得2a+b=0,所以3a+b=2a+b+a=a>0,即可判定④.
由二次函数图象开口向上,得到a>0;与y轴交于负半轴,得到c<0,对称轴在y轴右侧,a、b异号,则b<0,所以abc>0,①正确;
②由图象可知,当x=0时,y<0,根据对称轴为x=1可得当x=2时,y<0,当x>2时,y值得符号不确定,∴②不正确;
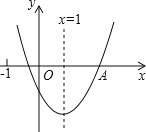
③∵当x=-1时,y>0,
∴a-b+c=0,
∵-![]() =1,
=1,
∴b=-2a,
∴a+2a+c>0,
∴3a+c>0,
∴③正确;
④∵-![]() =1,
=1,
∴2a+b=0,
∴3a+b=2a+b+a=a>0,
∴④正确.
综上,正确的结论为①③④.
故选C.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A(-2,4),B(4,2),在x轴上取一点P,使点P到点A和点B的距离之和最小,则点P的坐标是( )

A. (-2,0) B. (0,0) C. (2,0) D. (4,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明想了解全校3000名同学对新闻、体育、音乐、娱乐、戏曲五类电视节目的喜爱况,从中抽取了一部分同学进行了一次抽样调查,利用所得数据绘制成下面的统计图:根据图中所给信息,全校喜欢娱乐类节目的学生大约有( )人.

A. 1080 B. 900 C. 600 D. 108
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国共产党第十九次全国代表大会提出了要坚定实施七大战略,某数学兴趣小组从中选取了四大战略进行调查,A:科教兴国战略,B:人才强国战略,C:创新驱动发展战略,D:可持续发展战略,要求被调查的每位学生只能从中选择一个自已最关注的战略,根据调查结果,该小组绘制了如图所示的两幅不完整的统计图,请你根据统计图中提供的信息,解答下列问题:
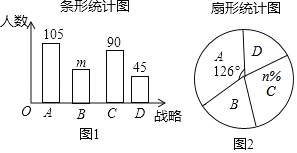
(1)求本次抽样调查的学生人数;
(2)求出统计图中m、n的值;
(3)在扇形统计图中,求战略B所在扇形的圆心角度数;
(4)若该校有3000名学生,请估计出选择战略A和B共有的学生数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年的![]() 月
月![]() 日是“国际消费者权益日”,许多商家都会利用这个契机进行打折促销活动.甲卖家的
日是“国际消费者权益日”,许多商家都会利用这个契机进行打折促销活动.甲卖家的![]() 商品成本为
商品成本为![]() 元,在标价
元,在标价![]() 元的基础上打
元的基础上打![]() 折销售.
折销售.
![]() 现在甲卖家欲继续降价吸引买主,问最多降价多少元,才能使利润率不低于
现在甲卖家欲继续降价吸引买主,问最多降价多少元,才能使利润率不低于![]() ?
?
![]() 据媒体爆料,有一些卖家先提高商品价格后再降价促销,存在欺诈行为.乙卖家也销售
据媒体爆料,有一些卖家先提高商品价格后再降价促销,存在欺诈行为.乙卖家也销售![]() 商品,成本、标价与甲卖家一致,以前每周可售出
商品,成本、标价与甲卖家一致,以前每周可售出![]() 件,为扩大销量,尽快减少库存,他决定打折促销.但他先将标价提高
件,为扩大销量,尽快减少库存,他决定打折促销.但他先将标价提高![]() ,再大幅降价
,再大幅降价![]() 元,使得
元,使得![]() 商品在
商品在![]() 月
月![]() 日那一天卖出的数量就比原来一周卖出的数量增加了
日那一天卖出的数量就比原来一周卖出的数量增加了![]() ,这样一天的利润达到了
,这样一天的利润达到了![]() 元,求
元,求![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,二次函数的图象与x轴交于A(-2,0),B(4,0)两点,且函数的最大值为9.
(1)求二次函数的解析式;

(2)设此二次函数图象的顶点为C,与y轴交点为D,求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】太平商场销售一批名牌![]() 恤,平均每天可售出
恤,平均每天可售出![]() 件,每件盈利
件,每件盈利![]() 元,为了扩大销售,增加盈利,商场决定采用适当的降价措施,经调查,如果每件
元,为了扩大销售,增加盈利,商场决定采用适当的降价措施,经调查,如果每件![]() 恤每降价
恤每降价![]() 元,商场平均每天多售出
元,商场平均每天多售出![]() 件,
件,
①若商场平均每天要盈利![]() 元,则每件
元,则每件![]() 恤应降价多少元?
恤应降价多少元?
②每件![]() 恤降价多少元时,商场平均每天盈利最多?最大盈利多少元?请说明你的理由.
恤降价多少元时,商场平均每天盈利最多?最大盈利多少元?请说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在同一平面直角坐标系中画出函数![]() 和
和![]() 的图象.
的图象.

![]() 观察图象,说出抛物线的顶点坐标、开口方向、对称轴;
观察图象,说出抛物线的顶点坐标、开口方向、对称轴;
![]() 说出各函数的最值;
说出各函数的最值;
![]() 说明各函数图象在对称轴两侧部分的函数值
说明各函数图象在对称轴两侧部分的函数值![]() 随
随![]() 的增大而变化的情况.
的增大而变化的情况.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com