
【题目】已知a>b,则下列不等式成立的是( )
A.a﹣c>b﹣c
B.a+c<b+c
C.ac>bc
D.![]()
科目:初中数学 来源: 题型:
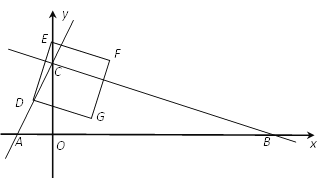
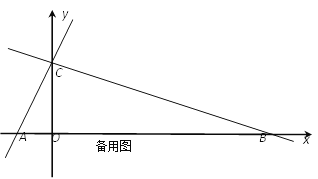
【题目】如图,在平面直角坐标系中,直线y=2x+4分别交x轴,y轴于点A,C,点D(m,2)在直线AC上,点B在x轴正半轴上,且OB=3OC.点E是y轴上任意一点记点E为(0,n).
(1)求直线BC的关系式;
(2)连结DE,将线段DE绕点D按顺时针旋转90°得线段DG,作正方形DEFG,是否存在n的值,使正方形DEFG的顶点F落在△ABC的边上?若存在,求出所有的n值并直接写出此时正方形DEFG与△ABC重叠部分的面积;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A(﹣m,n),B(0,m),且m、n满足 ![]() +(n﹣5)2=0,点C在y轴上,将△ABC沿y轴折叠,使点A落在点D处.
+(n﹣5)2=0,点C在y轴上,将△ABC沿y轴折叠,使点A落在点D处. 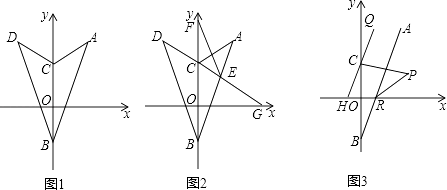
(1)写出D点坐标并求A、D两点间的距离;
(2)若EF平分∠AED,若∠ACF﹣∠AEF=20°,求∠EFB的度数;
(3)过点C作QH平行于AB交x轴于点H,点Q在HC的延长线上,AB交x轴于点R,CP、RP分别平分∠BCQ和∠ARX,当点C在y轴上运动时,∠CPR的度数是否发生变化?若不变,求其度数;若变化,求其变化范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,(10分)AB∥DE,试问∠B、∠E、∠BCE有什么关系.

解:∠B+∠E=∠BCE
过点C作CF∥AB,
则![]() ____( )
____( )
又∵AB∥DE,AB∥CF,
∴____________( )
∴∠E=∠____( )
∴∠B+∠E=∠1+∠2
即∠B+∠E=∠BCE.
查看答案和解析>>
科目:初中数学 来源: 题型:
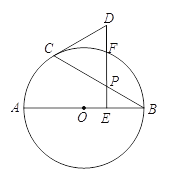
【题目】如图,AB是⊙O的直径,点P是弦BC上一动点(不与B,C重合),过点P作PE⊥AB,垂足为E,在射线EP上取点D使得DC=DP,连接DC.
(1)求证:DC是⊙O的切线;
(2)若∠CBA=30°,射线EP交⊙O于点 F,当点 F恰好是弧BC的中点时,判断以B,O,C,F为顶点的四边形是什么特殊四边形?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
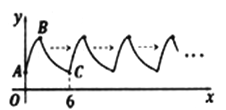
【题目】如图,曲线AB是顶点为B,与y轴交于点A的抛物线 ![]() 的一部分,曲线BC是双曲线
的一部分,曲线BC是双曲线![]() 的一部分,由点C开始不断重复“A-B-C”的过程,形成一组波浪线.点P(2017,m)与Q(2020,n)均在该波浪线上,
的一部分,由点C开始不断重复“A-B-C”的过程,形成一组波浪线.点P(2017,m)与Q(2020,n)均在该波浪线上, ![]() =_______.
=_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举办校级篮球赛,进入决赛的队伍有A、B、C、D,要从中选出两队打一场比赛.
(1)若已确定A打第一场,再从其余三队中随机选取一队,求恰好选中D队的概率.
(2)请用画树状图或列表法,求恰好选中B、C两队进行比赛的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了鼓励市民节约用水,某市水费实行分段计费制,每户每月用水量在规定用量及以下的部分收费标准相同,超出规定用量的部分收费标准相同.例如:若规定用量为10吨,每月用水量不超过10吨按1.5元/吨收费,超出10吨的部分按2元/吨收费,则某户居民一个月用水8吨,则应缴水费:8×1.5=12(元);某户居民一个月用水13吨,则应缴水费:10×1.5+(13﹣10)×2=21(元).
表是小明家1至4月份用水量和缴纳水费情况,根据表格提供的数据,回答:
月份 | 一 | 二 | 三 | 四 |
用水量(吨) | 6 | 7 | 12 | 15 |
水费(元) | 12 | 14 | 28 | 37 |
(1)该市规定用水量为 吨,规定用量内的收费标准是 元/吨,超过部分的收费标准是 元/吨.
(2)若小明家五月份用水20吨,则应缴水费 元.
(3)若小明家六月份应缴水费46元,则六月份他们家的用水量是多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,M为BC边上的中点,D是射线AM上的一个动点,以CD为一边且在CD的下方作等边△CDE,连接BE. 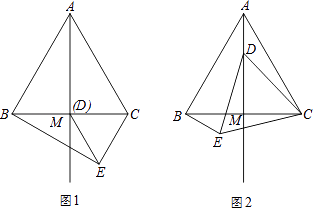
(1)填空:若D与M重合时(如图1)∠CBE=度;
(2)如图2,当点D在线段AM上时(点D不与A、M重合),请判断(1)中结论是否成立?并说明理由;
(3)在(1)的条件下,若AB=6,试求CE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com