
 张师傅驾车从甲地去乙地,途中在加油站加了一次油,加油时,车载电脑显示还能行驶50千米.假设加油前、后汽车都以100千米/小时的速度匀速行驶,已知油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如图所示.
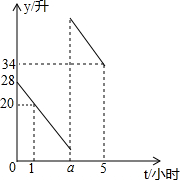
张师傅驾车从甲地去乙地,途中在加油站加了一次油,加油时,车载电脑显示还能行驶50千米.假设加油前、后汽车都以100千米/小时的速度匀速行驶,已知油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如图所示.分析 (1)直接利用待定系数法求出一次函数解析式进而得出答案;
(2)首先求出y=0时,t的值,进而得出a的值;
(3)根据汽车的耗油量以及剩余油量和加油量之间关系得出等式求出答案.
解答 解:(1)设加油前函数解析式为y=kt+b(k≠0),
把(0,28)和(1,20)代入,
得$\left\{\begin{array}{l}b=28\\ k+b=20\end{array}\right.$,
解得:$\left\{\begin{array}{l}k=-8\\ b=28\end{array}\right.$,
故张师傅加油前油箱剩余油量y(升)与行驶时间t(小时)之间的关系式为:y=-8t+28;
(2)当y=0时,-8t+28=0,
解得:t=$\frac{7}{2}$,
∵加油时,车载电脑显示还能行驶50千米,加油前、后汽车都以100千米/小时的速度匀速行驶,
∴剩余油量可以行使$\frac{50}{100}$小时,
故a=$\frac{7}{2}$-$\frac{50}{100}$=3;
(3)设途中加油x升,则28+x-34=8×$\frac{500}{100}$,
解得:x=46,
答:张师傅途中加油46升.
点评 此题主要考查了一次函数的应用,正确求出一次函数解析式是解题关键.


 互动英语系列答案
互动英语系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x2-x-2=(x-1)(x+2) | B. | -a2+a-$\frac{1}{4}$=$-\frac{1}{4}(2a-1)^{2}$ | ||
| C. | a(x-y)-b(y-x)=(x-y)(a-b) | D. | x2-4+2x=(x+2)(x-2)+2x |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com