
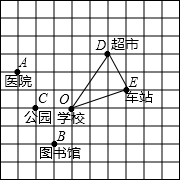
 如图,10×10的正方形网格(每个小正方形的边长为1)表示某市部分简图,学校,医院、图书馆、公园、超市、车站的位置分别用点O、A、B、C、D、E表示,请你完成下列问题:
如图,10×10的正方形网格(每个小正方形的边长为1)表示某市部分简图,学校,医院、图书馆、公园、超市、车站的位置分别用点O、A、B、C、D、E表示,请你完成下列问题:分析 (1)根据题意建立坐标系,写出各点坐标即可;
(2)作出各点关于x轴的对称点,再顺次连接即可;
(3)写出各点坐标,再用待定系数法求出直线AC的解析式,把点B的坐标代入进行检验即可.
解答  解:(1)如图,由图可知,A(-3,2),B(-1,-2).
解:(1)如图,由图可知,A(-3,2),B(-1,-2).
故答案为:(-3,2),(-1,-2);
(2)如图,△OD′E′即为所求;
(3)∵A(-3,2),B(-1,-2),C(-2,0),
∴设直线AC的解析式为y=kx+b(k≠0),
∴$\left\{\begin{array}{l}{-3k+b=2}\\{-2k+b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-2}\\{b=-4}\end{array}\right.$,
∴直线AC的解析式为y=-2x-4.
∵当x=-1时,y=2-4=-2,
∴点B在直线AC上,即医院、公园、图书馆所处的点位置在同一条直线上.
点评 本题考查的是作图-轴对称变换,熟知轴对称的性质是解答此题的关键.


 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 一段抛物线:y=-(x-$\frac{3}{2}$)2+$\frac{9}{4}$(0≤x≤3)记为C1,它与x轴交于点O,A1:将C1绕点A1旋转180°得到C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…如此进行下去,直至得C13,若P(37,m)在第13段抛物线C13上,则m=2.
一段抛物线:y=-(x-$\frac{3}{2}$)2+$\frac{9}{4}$(0≤x≤3)记为C1,它与x轴交于点O,A1:将C1绕点A1旋转180°得到C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…如此进行下去,直至得C13,若P(37,m)在第13段抛物线C13上,则m=2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
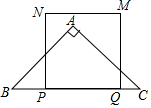 如图,在△ABC中,∠BAC=90°,AB=AC,BC=12cm,动点P从点B出发,以2cm/s的速度沿BC向点C运动,动点Q从点C出发,以1cm/s的速度沿CB向点B运动,当点P与Q相遇时,则同时停止运动,点P出发后,以线段PQ为边向上作正方形PQMN,设正方形PQMN与△ABC重叠部分图形的面积为S(cm2),点P的运动时间为t(s)
如图,在△ABC中,∠BAC=90°,AB=AC,BC=12cm,动点P从点B出发,以2cm/s的速度沿BC向点C运动,动点Q从点C出发,以1cm/s的速度沿CB向点B运动,当点P与Q相遇时,则同时停止运动,点P出发后,以线段PQ为边向上作正方形PQMN,设正方形PQMN与△ABC重叠部分图形的面积为S(cm2),点P的运动时间为t(s)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com