
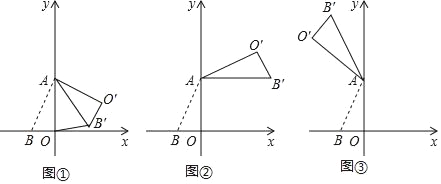
【题目】在平面直角坐标系中,O为原点,点A(0,4),点B(﹣2,0),把△ABO绕点A逆时针旋转,得△AB′O′,点B、O旋转后的对应点为B′、O′.
(1)如图①,若旋转角为60°时,求BB′的长;
(2)如图②,若AB′∥x轴,求点O′的坐标;
(3)如图③,若旋转角为240°时,边OB上的一点P旋转后的对应点为P′,当O′P+AP′取得最小值时,求点P′的坐标(直接写出结果即可)
【答案】(1)![]() ;(2)点O′的坐标为(
;(2)点O′的坐标为(![]() ,
,![]() +4);(3)点P′的坐标为(﹣
+4);(3)点P′的坐标为(﹣![]() ,
,![]() .
.
【解析】分析:(1)由点A、B的坐标可得出AB的长度,连接BB′,由旋转可知:AB=AB′,∠BAB′=60°,进而可得出△ABB′为等边三角形,根据等边三角形的性质可求出BB′的长;
(2)过点O′作O′D⊥x轴,垂足为D,交AB′于点E,则△AO′E∽△ABO,根据旋转的性质结合相似三角形的性质可求出AE、O′E的长,进而可得出点O′的坐标;
(3)作点A关于x轴对称的点A′,连接A′O′交x轴于点P,此时O′P+AP′取最小值,过点O′作O′F⊥y轴,垂足为点F,过点P′作PM⊥O′F,垂足为点M,根据旋转的性质结合解直角三角形可求出点O′的坐标,由A、A′关于x轴对称可得出点A′的坐标,利用待定系数法即可求出直线A′O′的解析式,由一次函数图象上点的坐标特征可得出点P的坐标,进而可得出OP的长度,再在Rt△O′P′M中,通过解直角三角形可求出O′M、P′M的长,进而可得出此时点P′的坐标.
详解:(1)∵点A(0,4),点B(﹣2,0),∴OA=4,OB=2,∴AB=![]() =2
=2![]() .
.
在图①中,连接BB′.
由旋转可知:AB=AB′,∠BAB′=60°,∴△ABB′为等边三角形,∴BB′=AB=2![]() .
.
(2)在图②中,过点O′作O′D⊥x轴,垂足为D,交AB′于点E.
∵AB′∥x轴,O′E⊥x轴,∴∠O′EA=90°=∠AOB.
由旋转可知:∠B′AO′=∠BAO,AO′=AO=4,∴△AO′E∽△ABO,![]() =
=![]() =
=![]() ,即
,即![]() =
=![]() =
=![]() ,∴AE=
,∴AE=![]() ,O′E=
,O′E=![]() ,∴O′D=
,∴O′D=![]() +4,∴点O′的坐标为(
+4,∴点O′的坐标为(![]() +4).
+4).
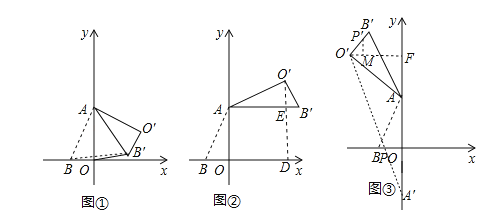
(3)作点A关于x轴对称的点A′,连接A′O′交x轴于点P,此时O′P+AP′取最小值,过点O′作O′F⊥y轴,垂足为点F,过点P′作PM⊥O′F,垂足为点M,如图3所示.
由旋转可知:AO′=AO=4,∠O′AF=240°﹣180°=60°,∴AF=![]() AO′=2,O′F=
AO′=2,O′F=![]() AO′=2
AO′=2![]() ,∴点O′(﹣2
,∴点O′(﹣2![]() ,6).
,6).
∵点A(0,4),∴点A′(0,﹣4).
设直线A′O′的解析式为y=kx+b,将A′(0,﹣4)、O′(﹣2![]() ,6)代入y=kx+b,得:
,6)代入y=kx+b,得:
![]() ,解得:
,解得: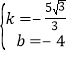 ,∴直线A′O′的解析式为y=﹣
,∴直线A′O′的解析式为y=﹣![]() x﹣4.
x﹣4.
当y=0时,有﹣![]() x﹣4=0,解得:x=﹣
x﹣4=0,解得:x=﹣![]() ,∴点P﹣
,∴点P﹣![]() ,0),∴OP=O′P′=
,0),∴OP=O′P′=![]() .
.
在Rt△O′P′M中,∠MO′P′=60°,∠O′MP′=90°,∴O′M=![]() O′P′=
O′P′=![]() ,P′M=
,P′M=![]() O′P′=
O′P′=![]() ,∴点P′的坐标为(﹣2
,∴点P′的坐标为(﹣2![]() +
+![]() ,6+
,6+![]() ),即(﹣
),即(﹣![]() ).
).


科目:初中数学 来源: 题型:
【题目】如图,AD是等腰△ABC底边BC上的高.点O是AC中点,延长DO到E,使OE=OD,连接AE,CE.
(1)求证:四边形ADCE的是矩形;
(2)若AB=17,BC=16,求四边形ADCE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小张同学在计算![]() 时,将“
时,将“![]() ”错看成了“
”错看成了“![]() ”,得出的结果是
”,得出的结果是![]() .
.
(1)请你求出这道题的正确结果;
(2)试探索:当字母![]() 、
、![]() 满足什么关系时,(1)中的结果与字母
满足什么关系时,(1)中的结果与字母![]() 的取值无关.
的取值无关.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+1经过A(-1,0),B(1,1)两点.
(1)求该抛物线的解析式;
(2)阅读理解:
在同一平面直角坐标系中,直线l1:y=k1x+b1(k1,b1为常数,且k1≠0),直线l2:y=k2x+b2(k2,b2为常数,且k2≠0),若l1⊥l2,则k1·k2=-1.
解决问题:
①若直线y=3x-1与直线y=mx+2互相垂直,求m的值;
②是否存在点P,使得△PAB是以AB为直角边的直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)M是抛物线上一动点,且在直线AB的上方(不与A,B重合),求点M到直线AB的距离的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() ABCD中,F是AD的中点,延长BC到点E,使CE=
ABCD中,F是AD的中点,延长BC到点E,使CE=![]() BC,连结DE,CF。
BC,连结DE,CF。

(1)求证:四边形CEDF是平行四边形;
(2)若AB=4,AD=6,∠B=60°,求DE的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两同学骑自行车从A地沿同一条路到B地,已知乙比甲先出发,他们离出发地的距离s(km)和骑行时间t(h)之间的函数关系如图所示,根据图像信息,以上说法正确的是( )
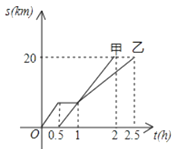
A.甲和乙两人同时到达目的地;B.甲在途中停留了0.5h;
C.相遇后,甲的速度小于乙的速度;D.他们都骑了20km
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有下列命题
①一组对边平行,一组对角相等的四边形是平行四边形.
②两组对角分别相等的四边形是平行四边形.
③一组对边相等,一组对角相等的四边形是平行四边形.
④一组对边平行,一条对角线被另一条对角线平分的四边形是平行四边形.
(1)上述四个命题中,是真命题的是 (填写序号);
(2)请选择一个真命题进行证明.(写出已知、求证,并完成证明)
已知: .
求证: .
证明:

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平行四边形ABCD在平面直角坐标系中的位置如图所示,其中A![]() ,
,![]() ,反比例函数
,反比例函数![]() 的图象经过点C.
的图象经过点C.
(1)求此反比例函数的解析式;
(2)将平行四边形ABCD沿x轴翻折得到平行四边形![]() ,请你通过计算说明点
,请你通过计算说明点![]() 在双曲线上.
在双曲线上.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com