
【题目】在平行四边形![]() 中,对角线
中,对角线![]() 、
、![]() 交于点
交于点![]() 、
、![]() 是
是![]() 上一点,连接
上一点,连接![]() ,点
,点![]() 在边
在边![]() 上,且
上,且![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,已知
,已知![]() ,
,![]() .
.
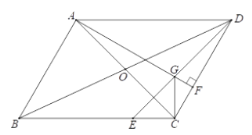
(1)若![]() ,
,![]() ,求
,求![]() 的长;
的长;
(2)求证:![]() .
.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
(1)延长CG交AD于N,连接NF,AC交DE于H,证出∠DGN=∠CGE=45°,GC⊥AD,得出∠GFD=90°=∠GND,证出N、G、F、D四点共圆,由圆周角定理得出∠NFG=∠NDG=45°,由∠ANC=∠AFC=90°,得出A、N、F、C四点共圆,由圆周角定理得出∠ACN=∠NFG=45°,得出∠CHD=90°,由直角三角形的性质得出DN=![]()
CD=2,CN=![]() DN=2
DN=2![]() ,得出AC=
,得出AC=![]() CN=2
CN=2![]() ;
;
(2)由(1)得:△ADH、△CGH是等腰直角三角形,由等腰直角三角形的性质即可得出结论.
(1)解:延长CG交AD于N,连接NF,AC交DE于H,如图所示:
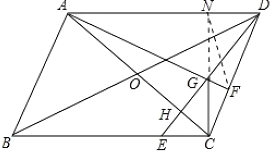
∵四边形ABCD是平行四边形,
∴AD∥BC,
∵GC⊥BC,∠DEC=45°,
∴∠DGN=∠CGE=45°,GC⊥AD,
∴∠GND=90°,
∴∠NDG=45°,
∵AF⊥CD,
∴∠GFD=90°=∠GND,
∴N、G、F、D四点共圆,
∴∠NFG=∠NDG=45°,
又∵∠ANC=∠AFC=90°,
∴A、N、F、C四点共圆,
∴∠ACN=∠NFG=45°,
∴∠CHD=45°+45°=90°,
∵CD=4,∠DCG=30°,
∴DN=![]()
CD=2,CN=![]() DN=2
DN=2![]() ,
,
∴AC=![]() CN=2
CN=2![]() ;
;
(2)证明:由(1)得:△ADH、△CGH是等腰直角三角形,
∴AD=![]() HD=
HD=![]() (HG+DG)=
(HG+DG)=![]() HG+
HG+![]() DG=CG+
DG=CG+![]() DG.
DG.


科目:初中数学 来源: 题型:
【题目】如图,直线 m,n 相交于 O,所夹的锐角是 53°,点 P,Q 分别是直线 m,n上的点,将直线 m,n 按照下面的程序操作,能使两直线平行的是( )

A. 将直线 m 以点 O 为中心,顺时针旋转 53° B. 将直线 n 以点 Q 为中心,顺时针旋转 53°
C. 将直线 m 以点 P 为中心,顺时针旋转 53° D. 将直线 m 以点 P 为中心,顺时针旋转 127°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家支持大学生创新办实业,提供小额无息贷款,学生王亮享受国家政策贷款36000元用于代理某品牌服装销售,已知该店代理的品牌服装的进价为每件40元,该品牌服装售量y(件)与销售价x(元/件)之间的关系可用图中的一条线段(实线)来表示.
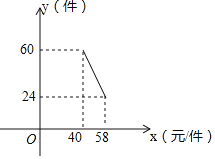
(1)求日销售量y与销售价x之间的函数关系式,并写出x的取值范围;
(2)该品牌服装售价x为多少元时,每天的销售利润W最大,且最大销售利润W为多少?
(3)若该店应支付员工的工资为每人每天82元,每天还应支付其它费用为106元(不包含贷款).现该店只有2名员工,则该店至少需要多少天才能还清所有贷款?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校计划开设四门选修课:乐器、舞蹈、绘画、书法.为提前了解学生的选修情况,学校采取随机抽样的方法进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门).对调查结果进行了整理,绘制成如下两幅不完整的统计图,请结合图中所给信息解答下列问题:
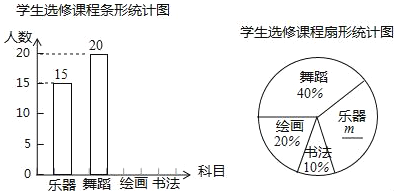
(1)本次调查的学生共有 人,在扇形统计图中,m的值是 ;
(2)将条形统计图补充完整;
(3)在被调查的学生中,选修书法的有2名女同学,其余为男同学,现要从中随机抽取2名同学代表学校参加某社区组织的书法活动,请直接写出所抽取的2名同学恰好是1名男同学和1名女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
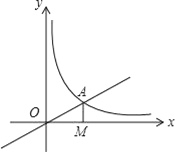
【题目】如图,直线OA:y=![]() x的图象与反比例函数y=
x的图象与反比例函数y=![]() (k≠0)在第一象限的图象交于A点,过A点作轴的垂线,垂足为M,已知△OAM的面积为1.
(k≠0)在第一象限的图象交于A点,过A点作轴的垂线,垂足为M,已知△OAM的面积为1.
(1)求反比例函数的解析式;
(2)如果B为反比例函数在第一象限图象上的点(点B与点A不重合),且B点的横坐标为1,在x轴上求一点P,使PA+PB最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x+
x+![]() 与双曲线y=
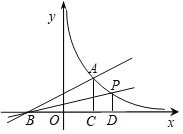
与双曲线y=![]() 在第一象限内的图象交于一点A(1,1),与x负半轴交与点B.点P(m,n)是该双曲线在第一象限内图象上的一点,且P点在A点的右侧,分别过点A、P作x轴的垂线,垂足分别为点C、D,连结PB.则△ABC的面积___△PBD的面积(填“<”、“=”或“>”).
在第一象限内的图象交于一点A(1,1),与x负半轴交与点B.点P(m,n)是该双曲线在第一象限内图象上的一点,且P点在A点的右侧,分别过点A、P作x轴的垂线,垂足分别为点C、D,连结PB.则△ABC的面积___△PBD的面积(填“<”、“=”或“>”).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点A为⊙0外一点,过A作⊙O的切线与⊙O相切于点P,连接PO并延长至圆上一点B连接AB交⊙O于点C,连接OA交⊙O于点D连接DP且∠OAP=∠DPA。
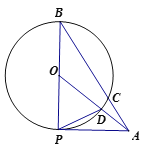
(1)求证:PO=PD
(2)若AC=![]() ,求⊙O的半径。
,求⊙O的半径。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场某种新商品每件进价是40元,在试销期间发现,当每件商品售价50元时,每天可销售500件,当每件商品售价高于50元时,每涨价5元,日销售量就减少50件。据此规律,请回答:
(1)当每件商品售价定为55元时,每天可销售多少件商品?商场获得的日盈利是多少?
(2)在上述条件不变,商品销售正常的情况下,每件商品的销售定价为多少元时,商场日盈利可达到8000元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com