
【题目】已知:如图,在矩形ABCD中,若CD=5,以D为圆心,DC长为半径作⊙D交CA的延长线于E,过D作DF⊥AC,垂足为F,且DF=3.
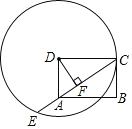
(1)求证:BC是⊙D的切线;
(2)求AE的长.
科目:初中数学 来源: 题型:
【题目】如图所示,矩形ABCD中,AB=5,BC=8,点P为BC上一动点(不与端点重合),连接AP,将△ABP沿着AP折叠.点B落到M处,连接BM、CM,若△BMC为等腰三角形,则BP的长度为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了鼓励城市周边的农民的种菜的积极性,某公司计划新建![]() ,
,![]() 两种温室80栋,将其售给农民种菜.已知建1个
两种温室80栋,将其售给农民种菜.已知建1个![]() 型温室和2个
型温室和2个![]() 型温室一共需要8.1万元,两种温室的成本和出售价如下表:
型温室一共需要8.1万元,两种温室的成本和出售价如下表:
|
| |
成本(万元/栋) | 2.5 |
|
出售价(万元/栋) | 3.1 | 3.5 |
(1)求![]() 的值;
的值;
(2)已知新建![]() 型温室不少于38栋不多于50栋且所建的两种温室可全部售出.为了减轻菜农负担,试问采用什么方案建设温室可使利润最少,最少利润是多少?
型温室不少于38栋不多于50栋且所建的两种温室可全部售出.为了减轻菜农负担,试问采用什么方案建设温室可使利润最少,最少利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
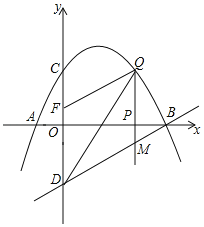
【题目】如图,已知抛物线y=﹣![]() +bx+c的图象经过点A(﹣1,0)和点C(0,2),点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q,交直线BD于点M.
+bx+c的图象经过点A(﹣1,0)和点C(0,2),点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q,交直线BD于点M.
(1)求该抛物线所表示的二次函数的表达式.
(2)已知点F(0,![]() ),当点P在x轴正半轴上运动时,试求m为何值时,四边形DMQF是平行四边形?
),当点P在x轴正半轴上运动时,试求m为何值时,四边形DMQF是平行四边形?
(3)点P在线段AB运动过程中,是否存在点Q,使得以点B、Q、M为顶点的三角形与△BOD相似?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
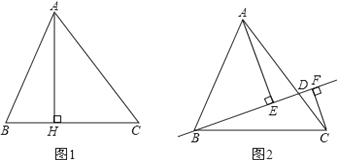
【题目】如图1和图2,在△ABC中,AB=13,BC=14,![]() .
.
探究:如图1,AH⊥BC于点H,则AH=___,AC=___,△ABC的面积![]() =___.
=___.
拓展:如图2,点D在AC上(可与点A、C重合),分别过点A、C作直线BD的垂线,垂足为E、F,设BD=x,AE=m,CF=n,(当点D与A重合时,我们认为![]() =0).
=0).
(1)用含x、m或n的代数式表示![]() 及
及![]() ;
;
(2)求(m+n)与x的函数关系式,并求(m+n)的最大值和最小值;
(3)对给定的一个x值,有时只能确定唯一的点D,指出这样的x的取值范围.
发现:请你确定一条直线,使得A、B、C三点到这条直线的距离之和最小(不必写出过程),并写出这个最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某品牌电脑销售公司有营销员14人,销售部为制定营销人员月销售电脑定额,统计了这14人某月的销售量如下(单位:台):
销售量 | 200 | 170 | 130 | 80 | 50 | 40 |
人数 | 1 | 1 | 2 | 5 | 3 | 2 |
(1)该公司营销员销售该品牌电脑的月销售平均数是 台,中位数是 台,众数是 台.
(2)销售部经理把每位营销员月销售量定为90台,你认为是否合理?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=10,AC=8,BC=6,直线l经过点A,且垂直于AB,分别与AB、AC相交于点M,N.直线l从点A出发,沿AB方向以1cm/s的速度向点B运动,当直线l经过点B时停止运动,若运动过程中△AMN的面积是y(cm2),直线l的运动时间是x(s)则y与x之间函数关系的图象大致是( )
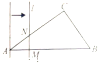
A.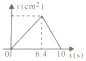 B.
B.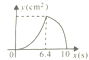
C.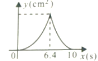 D.
D.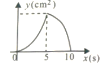
查看答案和解析>>
科目:初中数学 来源: 题型:
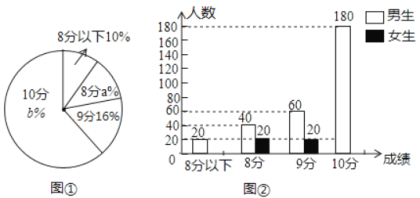
【题目】某中学对本校2018届500名学生的中考体育测试情况进行调查,根据男生1000米及女生800米测试成绩整理,绘制成不完整的统计图(图①,图②),请根据统计图提供的信息,解答下列问题:
(1)该校毕业生中男生有 人;扇形统计图中![]() ;500名学生中中考体育测试成绩的中位数是 ;
;500名学生中中考体育测试成绩的中位数是 ;
(2)补全条形统计图;
(3)从500名学生中随机抽取一名学生,这名学生该项成绩在8分及8分以下的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com