
【题目】问题背景:
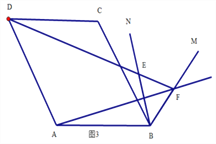
如图1,△ABC为等边三角形,作AD⊥BC于点D,将∠ABC绕点B顺时针旋转30°后,BA,BC边与射线AD分别交于点E,F,求证:△BEF为等边三角形.
迁移应用:
如图2,△ABC为等边三角形,点P是△ABC外一点,∠BPC=60°,将∠BPC绕点P逆时针旋转60°后,PC边恰好经过点A,探究PA,PB,PC之间存在的数量关系,并证明你的结论;
拓展延伸:
如图3,在菱形ABCD中,∠ABC=60°,将∠ABC绕点B顺时针旋转到如图所在的位置得到∠MBN,F是BM上一点,连接AF,DF,DF交BN于点E,若B,E两点恰好关于直线AF对称.
(1)证明△BEF是等边三角形;
(2)若DE=6,BE=2,求AF的长.


【答案】(1)见解析;(2) PC=PA+PB;(3)![]()
【解析】分析: (1)根据等边三角形的性质得到∠EBF=60°, 又由BD⊥AC得到∠BED=60°,从而得出结论; (2)在PC上截取PD=PB,连接BD,通过证明△APB≌△CBG得PA=GC,即可得出结论;(3) ①依据B,E两点关于直线AF对称得FE=FB,又由于∠EBF=60°即可得出结论; ②连接AE,过点A作AH⊥DE于点H,可得DH=3,HF=5, ∠EFA=30°,在Rt△AHF中,利用∠HFA的余弦即可求出AF的值.
详解:
(1)证明:∵△ABC为等边三角形,
∴AB=AC=BC,∠BAC=∠ABC=∠ACB=60°,
由题意得,∠ABE=30°,∠EBF=60°,
∴∠EBD=∠FBD=30°,
∵BD⊥AC,∴∠BED=60°,
∴△BEF为等边三角形;
(2) PC=PA+PB.
证明:在PC上截取PD=PB,连接BD,

∵∠BPC=60°,∴△BPG为等边三角形,
∴BG=BP,∠PBG=60°,PB=BG,
∴∠PBA+∠ABG=∠ABG+∠GBC=60°
∴∠PBA=∠GBC
又AB=BC,∴△APB≌△CBG,
∴PA=GC,
∴PC=PG+CG=PB+PA
(3)①∵B,E两点关于直线AF对称,∴FE=FB,
∵∠EBF=60°,∴△BEF是等边三角形;
②连接AE,过点A作AH⊥DE于点H,
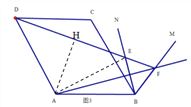
∵B,E两点关于直线AF对称,∴AE=AB,
∵四边形ABCD是菱形,∴AB=AD,
∴AE=AD,所以DH=HE=![]() DE=3,
DE=3,
∴HF=HE+EF=3+2=5,
由①知,△BEF是等边三角形,FA⊥EB,
∴∠EFA=![]() ∠EFB=30°
∠EFB=30°
.在Rt△AHF中,cos∠HFA=![]() =
=![]() ,
,
∴AF=![]() .
.
点睛:本题考查了等边三角形的性质,全等三角形的判定与性质以及三角函数, 解题的关键是正确作出辅助线,灵活运用三角形相似.


科目:初中数学 来源: 题型:
【题目】为了打造“书香校园”,明德华兴中学计划购买![]() 张书柜和一批书架(书架不少于
张书柜和一批书架(书架不少于![]() 只),现从
只),现从![]() 、
、![]() 两家超市了解到:同型号的产品价格相同,书柜每张
两家超市了解到:同型号的产品价格相同,书柜每张![]() 元,书架每只
元,书架每只![]() 元,
元,![]() 超市的优惠政策为每买一张书柜赠送一只书架,
超市的优惠政策为每买一张书柜赠送一只书架,![]() 超市的优惠政策为所有商品八折,设购买书架
超市的优惠政策为所有商品八折,设购买书架![]() 只
只![]() .
.
(1)若规定只能到其中一个超市购买所有物品,当购买书架多少只时,到两家超市购买所需费用一样;
(2)若学校想购买![]() 张书柜和
张书柜和![]() 只书架,且可到两家超市自由选购,你认为至少要准备多少货款,请用计算的结果来验证你的说法.
只书架,且可到两家超市自由选购,你认为至少要准备多少货款,请用计算的结果来验证你的说法.
查看答案和解析>>
科目:初中数学 来源: 题型:
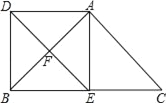
【题目】如图,E、F分别为△ABC的边BC、CA的中点,延长EF到D,使得DF=EF,连接DA、DB、AE.
(1)求证:四边形ACED是平行四边形;
(2)若AB=AC,试说明四边形AEBD是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自实施新教育改革后,学生的自主学习、合作交流能力有很大提高,张老师为了了解所教班级学生自主学习、合作交流的具体情况,对本班部分同学进行了为期半个月的跟踪调查,并将调查结果分为四类:A.特别好;B.好;C.一般;D.较差,并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:
(1)本次调查中,张老师一共调查了多少名同学?
(2)求出调查中C类女生及D类男生的人数,将条形统计图补充完整;
(3)为了共同进步,张老师想从被调查的A类和D类学生中分别选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,相距![]() 千米的
千米的![]() 两地间有一条笔直的马路,
两地间有一条笔直的马路,![]() 地位于
地位于![]() 两地之间且距
两地之间且距![]() 地
地![]() 千米,小明同学骑自行车从
千米,小明同学骑自行车从![]() 地出发沿马路以每小时
地出发沿马路以每小时![]() 千米的速度向
千米的速度向![]() 地匀速运动,当到达
地匀速运动,当到达![]() 地后立即以原来的速度返回,到达
地后立即以原来的速度返回,到达![]() 地停止运动,设运动时间为(时),小明的位置为点
地停止运动,设运动时间为(时),小明的位置为点![]() .
.
![]()
(1)当![]() 时,求点
时,求点![]() 间的距离
间的距离
(2)当小明距离![]() 地
地![]() 千米时,直接写出所有满足条件的
千米时,直接写出所有满足条件的![]() 值
值
(3)在整个运动过程中,求点![]() 与点
与点![]() 的距离(用含的代数式表示)
的距离(用含的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:O是直线AB上一点,∠AOC=50°,OD是∠BOC的角平分线,OE⊥OC于点O.求∠DOE的度数.(请补全下面的解题过程)

解:∵O是直线AB上一点,∠AOC=50°,
∴∠BOC=180°-∠AOC= °.
∵ OD是∠BOC的角平分线,
∴∠COD= ∠BOC .( )
∴∠COD=65°.
∵OE⊥OC于点O,(已知).
∴∠COE= °.( )
∴∠DOE=∠COE-∠COD= ° .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在△ABC中,AC=a,AB与BC所在直线成45°角,AC与BC所在直线形成的夹角的余弦值为![]() (即cosC=
(即cosC=![]() ),则AC边上的中线长是_____________.
),则AC边上的中线长是_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,射线BD是∠MBN的平分线,点A、C分别是角的两边BM、BN上两点,且AB=BC,E是线段BC上一点,线段EC的垂直平分线交射线BD于点F,连结AE交BD于点G,连结AF、EF、FC.

(1)求证:AF=EF;
(2)求证:△AGF∽△BAF;
(3)若点P是线段AG上一点,连结BP,若∠PBG=![]() ∠BAF,AB=3,AF=2,求
∠BAF,AB=3,AF=2,求![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在求两位数的平方时,可以用“列竖式”的方法进行速算,求解过程如图1所示.仿照图1,用“列竖式”的方法计算一个两位数的平方,部分过程如图2所示,若这个两位数的个位数字为a,则这个两位数为( )
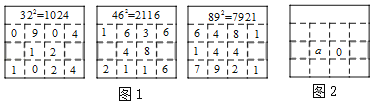
A.a﹣50B.a+50C.a﹣20D.a+20
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com