
【题目】(1)如图 ,∠AOB=∠COD=90°
①∠AOD=30°求∠BOC
②若∠AOD=α求用α的代数式表示∠BOC.

(2)如图2,若∠AOB=∠COD=60°,直接写出∠AOC与∠BOD的关系.
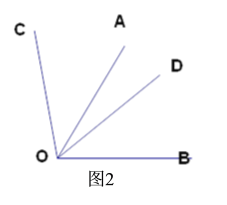
【答案】(1)①150°;②180°-α;(2)∠AOC=∠BOD.
【解析】
(1)①根据∠AOB=∠COD=90°,∠AOD=30°,∠AOC =∠COD-∠AOD=60°,进而求出∠BOC;
②根据∠AOB=∠COD=90°,∠AOD=α,∠AOC =∠COD-∠AOD=90°-α,进而求出∠BOC;;
(2)将∠AOB=∠COD=60°,写成∠AOD+∠BOD=∠AOD+∠AOC=60°,即可得出结论.
(1)①∵∠AOB=∠COD=90°,∠AOD=30°,
∴∠BOC=∠AOB+∠AOC
=∠AOB+(∠COD-∠AOD)
=90°+(90°-30°)
=150°;
②∵∠AOB=∠COD=90°,∠AOD=α,
∴∠BOC=∠AOB+∠AOC
=∠AOB+(∠COD-∠AOD)
=90°+(90°-α)
=180°-α;
(2)∠AOC=∠BOC,理由是:
∵∠AOB=∠COD=60°,
∴∠AOD+∠BOD=∠AOD+∠AOC,
∴∠AOC=∠BOD.


 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,![]() ,顶点C的坐标为
,顶点C的坐标为![]() ,x反比例函数
,x反比例函数![]() 的图象与菱形对角线AO交于点D,连接BD,当
的图象与菱形对角线AO交于点D,连接BD,当![]() 轴时,k的值是______.
轴时,k的值是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学决定在本校学生中开展足球、篮球、羽毛球、乒乓球四种活动,为了了解学生对这四种活动的喜爱情况,学校随机调查了该校m名学生,看他们喜爱哪一种活动(每名学生必选一种且只能从这四种活动中选择一种),现将调查的结果绘制成如下不完整的统计图.请你根据图中的信息,解答下列问题.
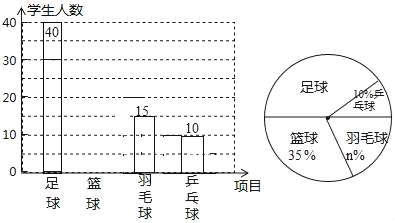
(1)m= ,n= ;
(2)请补全图中的条形图;
(3)扇形统计图中,足球部分的圆心角是 度;
(4)根据抽样调查的结果,请估算全校1800名学生中,大约有多少人喜爱踢足球.
查看答案和解析>>
科目:初中数学 来源: 题型:
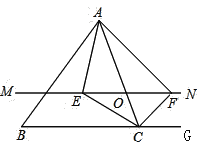
【题目】如图,在![]() 中,点
中,点![]() 是
是![]() 边上的一个动点,过点
边上的一个动点,过点![]() 作直线
作直线![]() ,设
,设![]() 交
交![]() 的角平分线于点
的角平分线于点![]() ,交
,交![]() 的外角平分线于点
的外角平分线于点![]() .
.
(1)求证:![]() ;
;
(2)当点![]() 运动到何处时,四边形
运动到何处时,四边形![]() 是矩形?并证明你的结论.
是矩形?并证明你的结论.
(3)当点![]() 运动到何处,且
运动到何处,且![]() 满足什么条件时,四边形
满足什么条件时,四边形![]() 是正方形?并说明理由.
是正方形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着通讯技术的迅猛发展,人与人之间的沟通方式更多样、便捷.某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:

(1)这次统计共抽查了 名学生;在扇形统计图中,表示“QQ”的扇形圆心角的度数为 ;
(2)将条形统计图补充完整;
(3)该校共有1500名学生,请估计该校最喜欢用“微信”进行沟通的学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,铁路MN和公路PQ在点O处交汇,∠QON=30°.公路PQ上A处距O点240米.如果火车行驶时,周围200米以内会受到噪音的影响.那么火车在铁路MN上沿ON方向以20米/秒的速度行驶时,A处受噪音影响的时间为( )

A. 16秒B. 18秒C. 20秒D. 22秒
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格中小正方形的边长为1,△ABC的三个顶点都在小正方形的格点上,求:
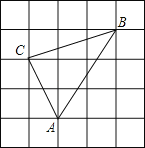
(1)△ABC的周长;
(2)请判断三角形ABC是否是直角三角形,并说明理由;
(3)△ABC的面积;
(4)点C到AB边的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程).有下列说法:

①“龟兔再次赛跑”的路程为1000米;
②兔子和乌龟同时从起点出发;
③乌龟在途中休息了10分钟;
④兔子在途中750米处追上乌龟.
其中正确的说法是 .(把你认为正确说法的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一张三角形纸片ABC中,AB=10cm,BC=7cm,AC=6cm,沿过点B的直线折叠这个三角形,使顶点C落在边AB上的点E处,折痕为BD.

(1)求△AED的周长.
(2)说明BD垂直平分EC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com