练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    17．下列说法中，正确的是（　　）
    A．$\sqrt{16}$=±4B．-22的平方根是±2
    C．64的立方根是±4D．-$\sqrt{5}$是5的一个平方根

    分析 依据算术平方根的性质、平方根的性质、立方根的性质求解即可．

    解答 解：A、$\sqrt{16}$=4，故A错误；
    B、-22=-4，负数没有平方根，故B错误；
    C、64的立方根是4，故C错误；
    D、-$\sqrt{5}$是5的一个平方根，故D正确．
    故选：D．

    点评 本题主要考查的是平方根、立方根、算术平方根的性质，熟练掌握相关知识是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

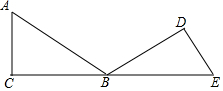    7．如图，在△ABC 中，∠ACB=90°，∠ABC=30°，将△ABC 绕顶点B顺时针旋转，使得点A与CB的延长线上的点E重合．
    （1）求旋转角的度数；     
    （2）连接CD，判断△CBD的形状，并求出∠BDC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．在直角坐标系中，点P（-3，2）向右平移4个单位长度后的坐标为（　　）
    A．（-3，6）B．（1，6）C．（1，2）D．（4，2）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．计算：
    （1）-9+（+$\frac{4}{5}$）-（-12）+（-5）+（-$\frac{4}{5}$）
    （2）（1-1$\frac{1}{2}$-$\frac{3}{8}$+$\frac{7}{12}$）×（-24）
    （3）-$\frac{5}{2}$+$\frac{28}{5}$÷（-2）×（-$\frac{5}{14}$）
    （4）-14-（1-$\frac{1}{2}$）÷3×|3-（-3）2|

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

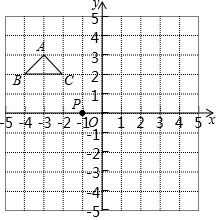    12．在建立平面直角坐标系的方格纸中，每个小方格都是边长为1的小正方形，△ABC的顶点均在格点上，点P的坐标为（-1，0），请按要求画图与作答：
    （1）把△ABC绕点P旋转180°得△A′B′C．
    （2）把△ABC向右平移7个单位得△A″B″C″．
    （3）△A′B′C与△A″B″C″是否成中心对称，若是，找出对称中心P′，并写出其坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    2．我国宋朝数学家杨辉在他的著作《详解九章算法》中提出“杨辉三角”（如图），此图揭示了（a+b）n（n为非负整数）展开式的项数及各项系数的有关规律．
    例如：（a+b）0=1，它只有一项，系数为1；
    （a+b）1=a+b，它有两项，系数分别为1，1，系数和为2；
    （a+b）2=a2+2ab+b2，它有三项，系数分别为1，2，1，系数和为4；
    （a+b）3=a3+3a2b+3ab2+b3，它有四项，系数分别为1，3，3，1，系数和为8；
    …
    根据以上规律，解答下列问题：
    （1）（a+b）4展开式共有5项，系数分别为1，4，6，4，1；
    （2）写出（a+b）5的展开式：（a+b）5=a5+5a4b+10a3b2+10a2b3+5ab4+b5；
    （3）（a+b）n展开式共有（n+1）项，系数和为2n．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．函数y=$\sqrt{x-2}$+$\frac{1}{{x}^{2}}$中自变量x的取值范围x≥2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．下列各数中：0，$\sqrt{8}$，1.3030030003…（每两个3之间多一个0），-1+$\sqrt{4}$，1.$\stackrel{•}{5}$4$\stackrel{•}{2}$，$\root{3}{-27}$，$\frac{22}{7}$，π2-3，无理数的个数有（　　）
    A．2个B．3个C．4个D．5个

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．如图．在平而直角坐标系中，已知A（0，2），B（$\frac{b-1}{2}$，0）将点B向上平移4个单位得到点C，其中b与4的差的2倍等于6
    （1）请直接写出B，C两点坐标；
    （2）如果在第二象限内有一点P（t，$\frac{2}{3}$），求四边形ABOP的面积（用含t的式子表示）
    （3）在（2）的条件下，若存在点P，使四边形ABOP的面积是△ABC面积的$\frac{3}{4}$，求点的P的坐标．

    查看答案和解析>>

    同步练习册答案