
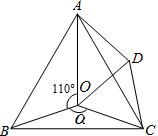
 如图,点O是等边△ABC内一点.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.已知∠AOB=110°.
如图,点O是等边△ABC内一点.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.已知∠AOB=110°.分析 (1)利用有一个角为60°的等腰三角形为等边三角形即可得证;
(2)三角形AOD为直角三角形,理由为:由旋转得到两三角形全等,进而求出∠ADC=∠BOC=150°,再由三角形COD为等边三角形,进而确定出∠ADO为直角,即可得证.
解答 (1)证明:∵CO=CD,∠OCD=60°,
∴△COD是等边三角形;
(2)解:当α=150°,即∠BOC=150°时,△AOD是直角三角形.
∵△BOC≌△ADC,
∴∠ADC=∠BOC=150°,
又∵△COD是等边三角形,
∴∠ODC=60°,
∴∠ADO=90°,
即△AOD是直角三角形.
点评 此题考查了旋转的性质,以及等边三角形的判定与性质,熟练掌握旋转的性质是解本题的关键.


科目:初中数学 来源: 题型:选择题
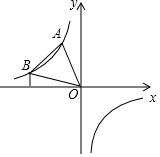 如图,已知A,B两点都在反比例函数y=-$\frac{8}{x}$位于第二象限内的图象上,且△OAB为等边三角形,则△OAB的面积为( )
如图,已知A,B两点都在反比例函数y=-$\frac{8}{x}$位于第二象限内的图象上,且△OAB为等边三角形,则△OAB的面积为( )| A. | 4$\sqrt{3}$cm2 | B. | 6$\sqrt{3}$cm2 | C. | 8$\sqrt{3}$cm2 | D. | 12$\sqrt{3}$cm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 男生序号 | ① | ② | ③ | ④ | ⑤ | ⑥ | ⑦ | ⑧ | ⑨ | ⑩ |
| 身高 | 163 | 171 | 173 | 159 | 161 | 174 | 164 | 166 | 169 | 164 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com