
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��y=x+3�ֱ�x�ᡢy����A��C���㣬������y=ax2+bx+c��a��0��������A��C���㣬��x�ύ�ڵ�B��1��0����
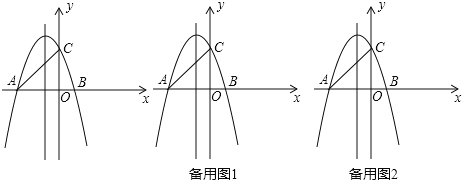
��1���������ߵĽ���ʽ��
��2����DΪֱ��AC��һ�㣬��EΪ��������һ�㣬��D��E����ĺ����궼Ϊ2����FΪx���ϵĵ㣬���ı���ADEF��ƽ���ı��Σ���ֱ��д����F�����ꣻ
��3������P���߶�AC�ϵ�һ�����㣬����P��x��Ĵ��ߣ����������ڵ�Q������AQ��CQ������ACQ����������ֵ��
���𰸡���1��y=��x2��2x+3����2����7��0������3��![]() ��
��
��������
�����������1����x=0����ֱ�ߵĽ���ʽ��õ�C��0��3������y=0�������x=��3���Ӷ��õ���A����3��0�����������ߵĽ���ʽΪy=a��x+3����x��1��������C�������������a=��1���Ӷ��õ������ߵĽ���ʽΪy=��x2��2x+3��
��2����x=2�ֱ����ֱ�ߺ������ߵĽ���ʽ����õ�D��2��5����E��2����5����Ȼ�����ƽ���ı��εĶԽ�����ƽ�ֿ���õ�F�����ꣻ
��3����ͼ2��ʾ�����P������Ϊ��a��a+3�������Q������Ϊ��a����a2��2a+3����QP=��a2��3a���������ε������ʽ��֪����ACQ�����=![]() ��
��![]() Ȼ�������䷽����ö��κ��������ֵ����
Ȼ�������䷽����ö��κ��������ֵ����
�⣺��1������x=0����y=x+3����y=3��
����C��������0��3����
����y=0����y=x+3�õ�x=��3��
����A����������3��0����
�������ߵĽ���ʽΪy=a��x+3����x��1��������C���������ã���3a=3��
��ã�a=��1��
�������ߵĽ���ʽΪy=����x+3����x��1����
�����ã�y=��x2��2x+3��
��2������x=2����y=x+3�ã�y=5��
����D��2��5����
��x=2����y=��x2��2x+3�ã�y=��5��
����E��������2����5����
��ͼ1��ʾ��
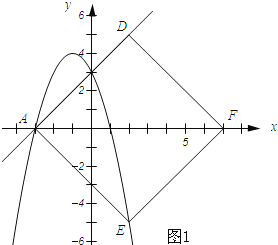
���ı���ADFEΪƽ���ı��Σ�
����F��������7��0����
��3����ͼ2��ʾ��
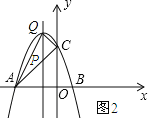
���P��������a��a+3�������Q��������a����a2��2a+3����
QP=��a2��2a+3����a+3��=��a2��2a+3��a��3=��a2��3a��
�ߡ�ACQ�����=![]() ��
��
���ACQ�����=![]() =
=![]() ��
��![]() =
=![]() ��a
��a![]() ��2+
��2+![]() ��
��
���ACQ����������ֵΪ![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=ax2+bx+c��ͼ����ͼ��ʾ��OA=OC�����������ߵ�����д�����º���a��b��c������ĸ�ĵ�ʽ��ʽ����![]() =��1����ac+b+1=0����abc��0����a��b+c��0��������ȷ�ĸ����ǣ��� ��
=��1����ac+b+1=0����abc��0����a��b+c��0��������ȷ�ĸ����ǣ��� ��
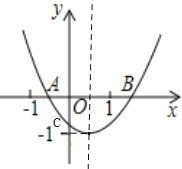
A. 4�� B. 3�� C. 2�� D. 1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������y=x2-2x-3��x�ύ��A��B������
��1����0��x��3ʱ����y��ȡֵ��Χ��
��2����PΪ��������һ�㣬��S��PAB=10�������ʱ��P�����꣮
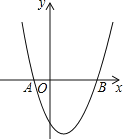
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��������������A��B��C��ͬһ��·�����ס��������οʹӾ���A�������ײ��е�����C;�ҳ˾����۹�ȵ�����B����B��ͣ��һ��ʱ������ٲ��е�����C���ס�������ͬʱ���ᄚ��C���ס������˾ྰ��A��·��y(��)��׳�����ʱ��x(��)֮��ĺ���ͼ����ͼ��ʾ��

��1���Ҳ��е��ٶ�Ϊ_ __��/����
��2�����ҳ˾����۹ʱy��x֮��ĺ�����ϵʽ��
��3���׳����ʱ�����ҵ�һ������?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC������A����B����C�ĶԱ߷ֱ��Ϊ![]() ��
��![]() ��
��![]() �����������������ж���ABCΪֱ�������ε����� ����
�����������������ж���ABCΪֱ�������ε����� ����
A����A+��B=��C
B����A�á�B�á�C =1��2��3
C��![]()
D��![]() ��
��![]() ��
��![]() =3��4��6
=3��4��6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��̨����һ����Ȼ�ֺ�������̨������ΪԲ�ģ�����Χ��ʮǧ��Χ���������籩���м�ǿ���ƻ�������ʱij̨�������ں��� B �������غ����� A �����Ϸ��� 240 ǧ�ף������ķ���Ϊ12 ����ÿԶ��̨������ 25 ǧ�ף�̨��ͻ����һ������ͼ��ʾ����̨���������� 20 ǧ��/ʱ���ٶ��� BC �����ƶ�����֪ AD��BC ��AD= ![]() AB����̨�����ĵķ������䣬���������ܷ����ﵽ�� 4 ���������̨��Ӱ�죮���ʣ�
AB����̨�����ĵķ������䣬���������ܷ����ﵽ�� 4 ���������̨��Ӱ�죮���ʣ�

��1��A �����Ƿ���ܵ�̨��Ӱ�죿��˵�����ɣ�
��2�������ܵ�̨��Ӱ�죬��ǫ̂��Ӱ��ó��еij���ʱ���ж��
��3���ó����ܵ�̨��Ӱ���������Ϊ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�������Ŀڴ���װ��4���ֱ�������֩�1����2��3��4��С�����ǵ���״����С��ȫ��ͬ��С���ȴӿڴ����������һ��С���������Ϊx��Сӱ��ʣ�µ�3��С�����������һ��С���������Ϊy��
��1��С��������������3��С��ĸ����� ��
��2�������б�������״ͼ�ķ�����ʾ����x��yȷ���ĵ�P��x��y�����п��ܵĽ�����������P��x��y���������������ĸ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͼ1��һ����Ϊ2m����Ϊ2n�ij����Σ����ó�������ͼ�������ü������ֳ��Ŀ�С�����Σ�Ȼ����ͼ2��ʾƴ��һ�������Σ�
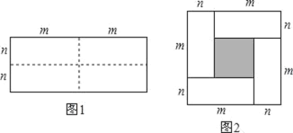
��1��ʹ�ò�ͬ��������ͼ2��С�����ε���������Ƴ���m+n��2����m-n��2��mn֮��ĵ�����ϵΪ�� ��
��2�����ã�1���еĽ��ۣ�����������⣺
����֪a-b��4��ab��5����a+b��ֵ��
����֪a��0��a-![]() ��2����a+
��2����a+![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��A��6, 0����B��0, 4������B����x��ĶԳƵ�ΪC�㣬��D��x��ĸ������ϣ���ABD�������30.
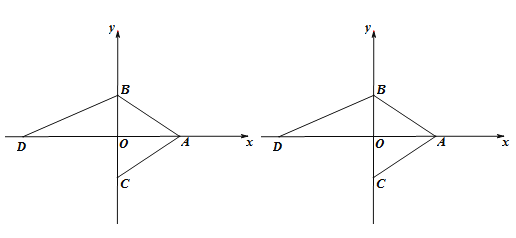
��1�����D����.
��2��������P�ӵ�B������������BC�˶����ٶ�Ϊÿ��1����λ����P���˶�ʱ��Ϊt�룬��APC�����ΪS����S��t�Ĺ�ϵʽ.
��3���ڣ�2���������£�ͬʱ��Q��D�������x����������ÿ��2����λ�ٶ������˶�������R�ڹ�A����ƽ����y���ֱ���ϣ�����PQRΪ��PQΪֱ�DZߵĵ���ֱ��������ʱ��������������tֵ����ֱ��д����R������.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com