练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】两组邻边分别相等的四边形叫做“筝形”，如图，四边形ABCD是一个筝形，其中，，詹姆斯在探究筝形的性质时，得到如下结论：
    ；；≌；四边形ABCD的面积其中正确的结论有　　

    A. 1个 B. 2个 C. 3个 D. 4个

    【答案】D

    【解析】

    先证明△ABD与△CBD全等，再证明△AOD与△COD全等即可判断．

    在△ABD与△CBD中，

    ，

    ∴△ABD≌△CBD（SSS），

    故③正确；

    ∴∠ADB=∠CDB，

    在△AOD与△COD中，

    ，

    ∴△AOD≌△COD（SAS），

    ∴∠AOD=∠COD=90°，AO=OC，

    ∴AC⊥DB，

    故①②正确；

    四边形ABCD的面积=S△ADB+S△BDC=DB×OA+DB×OC=ACBD，

    故④正确；

    故选：D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

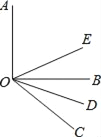
    【题目】如图所示，OE，OD分别平分∠AOC和∠BOC，

    （1）如果∠AOB=90°，∠BOC=38°，求∠DOE的度数；

    （2）如果∠AOB=α，∠BOC=β（α、β均为锐角，α＞β），其他条件不变，求∠DOE；

    （3）从（1）、（2）的结果中，你发现了什么规律，请写出来．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

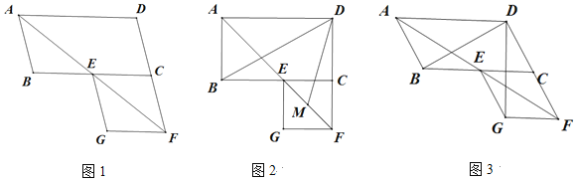
    【题目】在平行四边形ABCD中，∠BAD的平分线交线段BC于点E，交线段DC的延长线于点F，以EC、CF为邻边作平行四边形ECFG．

    （1）如图1，证明平行四边形ECFG为菱形；

    （2）如图2，若∠ABC=90°，M是EF的中点，求∠BDM的度数；

    （3）如图3，若∠ABC=120°，请直接写出∠BDG的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】水果市场将120吨水果运往各地商家，现有甲、乙、丙三种车型供选择，每辆车的运载能力和运费如下表所示：(假设每辆车均满载)

    车型

    甲

    乙

    丙

    汽车运载量(吨/辆)

    5

    8

    10

    汽车运费(元/辆)

    400

    500

    600

    （1）若全部水果都用甲、乙两种车型来运送，需运费8200元，问分别需甲、乙两种车型各几辆？

    （2）为了节约运费，市场可以调用甲、乙、丙三种车型参与运送（每种车型至少1辆），已知它们的总辆数为16辆，你能通过列方程组的方法分别求出几种车型的辆数吗？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB=AC，∠ABC=45°，以AB为直径的⊙O交BC于点D，若BC=4 ，则图中阴影部分的面积为（ ）
    A.π+1
    B.π+2
    C.2π+2
    D.4π+1

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在矩形ABCD中，点E是CD的中点，点F是BC上一点，且FC=2BF，连接AE，EF．若AB=2，AD=3，则cos∠AEF的值是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在等边三角形ABC中，点D，E分别在边BC，AC上，且DE∥AB，过点E作EF⊥DE，交BC的延长线于点F.

    （1）求∠F的度数；

    （2）若CD=2，求DF的长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校八年级全体320名学生在电脑培训前后各参加了一次水平相同的考试，考分都以同一标准划分成“不合格”、“合格”、“优秀”三个等级．为了了解电脑培训的效果，用抽签方式得到其中32名学生的两次考试考分等级，所绘制的统计图如图所示．试结合图示信息回答下列问题：

    （1）这32名学生培训前考分的中位数所在的等级是 ，培训后考分的中位数所在的等级是 ．

    （2）这32名学生经过培训，考分等级“不合格” 的百分比由 下降到 ．

    （3）估计该校整个八年级中，培训后考分等级为“合格”与“优秀”的学生共有 名．

    （4）你认为上述估计合理吗：理由是什么？

    答： ，理由： ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】认真阅读下面关于三角形内外角平分线所夹角的探究片段，完成所提出的问题.

    探究1：如图l，在△ABC中，O是∠ABC与∠ACB的平分线BO和CO的交点，通过分析发现∠BOC=90+∠A,理由如下：

    ∵BO和CO分别是∠ABC和∠ACB的角平分线

    ∴∠1=∠ABC, ∠2=∠ACB

    ∴∠l+∠2=(∠ABC+∠ACB)= (180-∠A)= 90-∠A

    ∴∠BOC=180-(∠1+∠2) =180-(90-∠A)=90+∠A

    (1)探究2；如图2中，O是∠ABC与外角∠ACD的平分线BO和CO的交点，试分析∠BOC与∠A有怎样的关系？请说明理由．

    (2)探究3：如图3中, O是外角∠DBC与外角∠ECB的平分线BO和CO的交点，则∠BOC与∠A有怎样的关系？（直接写出结论）

    (3)拓展：如图4，在四边形ABCD中，O是∠ABC与∠DCB的平分线BO和CO的交点，则∠BOC与∠A+∠D有怎样的关系？（直接写出结论）

    查看答案和解析>>

    同步练习册答案