
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
| (x1+x2)2-4x1x2 |
| b2+12 |
| 1 |
| x |
| x |
| 1 | ||
|
| 1 |
| x |
| 1 |
| x |


科目:初中数学 来源:2012届初中毕业生学业考试(湖北黄石卷)数学(带解析) 题型:解答题
已知抛物线 的函数解析式为
的函数解析式为 ,若抛物线
,若抛物线 经过点
经过点
【小题1】求抛物线 的顶点坐标
的顶点坐标
【小题2】已知实数 ,请证明:
,请证明: ≥
≥ ,并说明
,并说明 为何值时才会有
为何值时才会有 .
.
【小题3】若抛物线先向上平移4个单位,再向左平移1个单位后得到抛物线 ,设
,设 用含有
用含有 的表达式表示出△
的表达式表示出△ 的面积
的面积 ,并求出
,并求出 的最小值及
的最小值及 取最小值时一次函数
取最小值时一次函数 的函数解析式。
的函数解析式。
(参考公式:在平面直角坐标系中,若 ,则
,则 ,
, 两点间的距离为)
两点间的距离为)
查看答案和解析>>
科目:初中数学 来源:2013届湖北省荆州市初中升学模拟考试数学试卷(带解析) 题型:解答题
已知抛物线的函数解析式为y=ax2+b x-3a(b<0),若这条抛物线经过点(0,-3),方程ax2+b x-3a=0的两根为x1,x2,且|x1-x2|=4.
⑴求抛物线的顶点坐标.
⑵已知实数x>0,请证明x+ ≥2,并说明x为何值时才会有x+
≥2,并说明x为何值时才会有x+ =2.
=2.
查看答案和解析>>
科目:初中数学 来源:2013年湖北省荆州市中考数学模拟试卷(一)(解析版) 题型:解答题
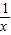 ≥2,并说明x为何值时才会有x+
≥2,并说明x为何值时才会有x+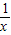 =2.
=2.查看答案和解析>>
科目:初中数学 来源:2012-2013学年湖北省荆州市升学模拟考试数学试卷(解析版) 题型:解答题
已知抛物线的函数解析式为y=ax2+b x-3a(b<0),若这条抛物线经过点(0,-3),方程ax2+b x-3a=0的两根为x1,x2,且|x1-x2|=4.
⑴求抛物线的顶点坐标.
⑵已知实数x>0,请证明x+ ≥2,并说明x为何值时才会有x+
≥2,并说明x为何值时才会有x+ =2.
=2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com