练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    17．将下列多项式因式分解
    （1）x2-10x-24
    （2）4x2y-12xy2+9y3
    （3）2（x-y）3-（y-x）2．

    分析 （1）原式利用十字相乘法分解即可；
    （2）原式提取y，再利用完全平方公式分解即可；
    （3）原式变形后，提取公因式即可得到结果．

    解答 解：（1）原式=（x+2）（x-12）；
    （2）原式=y（4x2-12xy+9y2）=y（2x-3y）2；
    （3）原式=2（x-y）3-（x-y）2=（x-y）2（2x-2y-1）．

    点评 此题考查了提公因式法与公式法的综合运用，熟练掌握因式分解的方法是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    7．阅读材料：
    对于平面内的任意两点A（x1，y1），B（x2，y2），
    由勾股定理易知A、B两点间的距离公式为：
    AB=${\sqrt{{{（{{x_2}-{x_1}}）}^2}+{{（{{y_2}-{y_1}}）}^2}}^{\;}}$．
    如：已知P1（-1，2），P2（0，3），
    则${P_1}{P_2}=\sqrt{{{（-1-0）}^2}+{{（2-3）}^2}}=\sqrt{2}$
    解答下列问题：
    已知点E（6，10），F（0，2），C（0，1）．
    （1）直接应用平面内两点间距离公式计算，
    E、F之间的距离为10及代数式$\sqrt{{x^2}+{{（{y-2}）}^2}}+\sqrt{{{（{x-6}）}^2}+{{（{y-10}）}^2}}$的最小值为10；
    （2）求以C为顶点，且经过点E的抛物线的解析式；
    （3）①若点D是上述抛物线上的点，且其横坐标为-3，试求DF的长；
    ②若点P是该抛物线上的任意一点，试探究线段FP的长度与点P纵坐标的数量关系，并证明你的猜想．
    ③我们知道“圆可以看成是所有到定点的距离等于定长的点的集合”．类似地，抛物线可以看成是到定点的距离等于到定直线的距离的点的集合．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．如图，在正方形ABCD中，点P是对角线AC上一点，过点P分别作AB、BC的垂线，垂足为E、F，连接EF．求证：PD=EF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．在学校组织的体育训练活动中，小明和小亮参加了举重训练，在近5次的测试中，所测成绩如图所示，请根据图中的信息解答以下问题：
    第1次第2次第3次第4次第5次
    小明（kg）105107.5105102.5105
    小亮（kg）102.5107.5100110105
    （1）将表格填写完整；
    （2）指出小明和小亮哪次成绩最好？
    （3）如果从他们两人中挑选1人参加比赛，你认为挑选谁参加比赛更有优势？简单说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．下列因式分解变形中，正确的是（　　）
    A．3（x-y）2+2（y-x）=（y-x）（3x-3y+2）B．6（m+n）2-2（m+n）=（2m+n）（3m+n+1）
    C．-2a2+4a-2=-2（a+1）2D．ab（a-b）-a（b-a）=-a（b-a）（b+1）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    2．已知一个三角形的面积为3x2-6xy+9x，其中一条边上的高是6x，则这条边的长是x-2y+3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．数据2，4，3，4，5，3，4的众数是（　　）
    A．2B．3C．4D．5

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．先化简：（$\frac{1}{x-1}$-$\frac{1}{x+1}$）÷$\frac{x}{{x}^{2}-1}$，再从-2，-1，0，1中选择一个恰当的数作为x的值，代入求出代数式的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

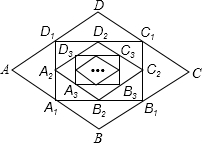    7．如图，在菱形ABCD中，边长为10，∠A=60°，顺次连接菱形ABCD各边中点，可得四边形A1B1C1D1；顺次连结四边形A1B1C1D1各边中点，可得四边形A2B2C2D2；顺次连结四边形A2B2C2D2各边中点，可得四边形A3B3C3D3；按此规律继续下去…．则四边形A2B2C2D2的周长是20；四边形A2015B2015C2015D2015的周长$\frac{5+5\sqrt{3}}{{2}^{1006}}$．

    查看答案和解析>>

    同步练习册答案