练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    1．已知$\sqrt{11-{x^3}}+\sqrt{2+{x^3}}$=5，则$\sqrt{11-{x^3}}-2\sqrt{2+{x^3}}$=-4或-1．

    分析 利用完全平方公式得出$\sqrt{11-{x}^{3}}$•$\sqrt{2+{x}^{3}}$=6，即可求出$\sqrt{11-{x}^{3}}$=2，$\sqrt{2+{x}^{3}}$=3或$\sqrt{11-{x}^{3}}$=3，$\sqrt{2+{x}^{3}}$=2．分别代入求解即可．

    解答 解：∵$\sqrt{11-{x^3}}+\sqrt{2+{x^3}}$=5，
    ∴（$\sqrt{11-{x^3}}+\sqrt{2+{x^3}}$）2=25，解得$\sqrt{11-{x}^{3}}$•$\sqrt{2+{x}^{3}}$=6，
    ∴解得$\sqrt{11-{x}^{3}}$=2，$\sqrt{2+{x}^{3}}$=3或$\sqrt{11-{x}^{3}}$=3，$\sqrt{2+{x}^{3}}$=2．
    ∴$\sqrt{11-{x^3}}-2\sqrt{2+{x^3}}$=-4或-1，
    故答案为：-4或-1．

    点评 本题主要考查了二次根式的化简求值，解题的关键是求出$\sqrt{11-{x}^{3}}$与$\sqrt{2+{x}^{3}}$的值．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    11．计算（1-$\frac{1}{{2}^{2}}$）（1-$\frac{1}{{3}^{2}}$）…（1-$\frac{1}{{9}^{2}}$）（1-$\frac{1}{1{0}^{2}}$）的值是$\frac{11}{20}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．如图，矩形OABC在平面直角坐标系中，点B的坐标为（4，3），直线l：y=-2x+b经过点A交x轴于点G．
    （1）直接填空：b=3；
    （2）直线l上有一个动点P．
    ①试探究|PB-PC|的最大值，并说明理由；
    ②若点P的横坐标为a（0＜a≤4），且△ACP的面积为S，试求S与a的函数关系式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．计算：（$\frac{1}{2}$）-2+（-2）3-20110=-5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

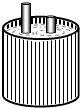    16．如图，两根铁棒直立于桶底水平的木桶中，在桶中加入水后，一根露出水面的长度是它的$\frac{1}{3}$，另一根露出水面的长度是它的$\frac{1}{5}$，两根铁棒长度之和为220cm，此时木桶中水的深度是80cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

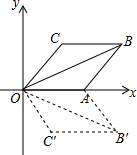    6．如图，菱形OABC的一边OA在x轴上，将菱形OABC沿x轴翻折到四边形OAB′C′的位置，若OB=2$\sqrt{3}$，∠C=120°，则点B′的坐标为（3，$-\sqrt{3}$）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

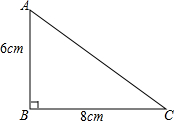    13．如图，在△ABC中，∠B=90°，AB=6cm，BC=8cm，点P从点A出发，以1cm/s的速度沿AB边向点B移动，以此同时，点Q从点C出发，以2cm/s的速度沿CB边向点B移动，如果P，Q同时出发，经过几秒，△PBQ的面积等于8cm2？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．已知点P（-2，4）与点Q关于原点对称，那么点Q的坐标是（2，-4）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

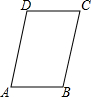    11．如图，已知四边形ABCD是平行四边形．
    （1）作∠A的平分线交BC于点E．（用尺规作图，保留作图痕迹，不用写作法）
    （2）在（1）中，若AD=6，EC=2，求平行四边形ABCD的周长．

    查看答案和解析>>

    同步练习册答案