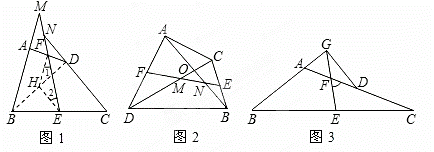
如图1，在四边形ABCD中，AB=CD，E、F分别是BC、AD的中点，连接EF并
延长，分别与BA、CD的延长线交于点M、N，则∠BME=∠CNE（不需证明）．
（温馨提示：在图1中，连接BD，取BD的中点H，连接HE、HF，根据三角形中位线定理，证明HE=HF，从而∠1=∠2，再利用平行线性质，可证得∠BME=∠CNE．）
问题一：如图2，在四边形ADBC中，AB与CD相交于点O，AB=CD，E、F分别是BC、AD的中点，连接EF，分别交DC、AB于点M、N，判断△OMN的形状，并说明理由；
问题二：如图3，在△ABC中，AC＞AB，D点在AC上，AB=CD，E、F分别是BC、AD的中点，连接EF并延长，与BA的延长线交于点G，若∠EFC=60°，连接GD，判断△AGD的形状并并说明理由．
科目：初中数学 来源： 题型：
下表是某地2012年2月与2013年2月8天同期的每日最高气温，根据表中数据回答问题：（单位：℃）
| 2日 | 4日 | 8日 | 10日 | 12日 | 14日 | 18日 | 20日 | |
| 2012年 | 12 | 13 | 14 | 22 | 6 | 8 | 9 | 12 |
| 2013年 | 13 | 13 | 12 | 9 | 11 | 16 | 12 | 10 |
（1）2012年2月气温的极差是 ，2013年2月气温的极差是 ．
由此可见， 年2月同期气温变化较大．
（2）2012年2月的平均气温是 ， 2013年2月的平均气温是 ．
（3）2012年2月的气温方差是 ， 2013年2月的气温方差是 ，
由此可见， 年2月气温较稳．
查看答案和解析>>
科目：初中数学 来源： 题型：
“种粮补贴”惠农政策的出台，大大激发了农民的种粮积极性，
某粮食生产专业户去年计划生产小麦和玉米共18吨，实际生产了20吨，其中
小麦超产12％，玉米超产10％．该专业户去年实际生产小麦、玉米各多少吨？
（1）根据题意，甲和乙两同学分别列出了如下不完整的方程组：
甲：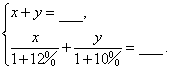
乙：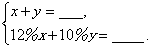
根据甲、乙两位同学所列的方程组，请你分别指出未知数x，y表示的意义，
然后在上面的横线上分别补全甲、乙两位同学所列的方程组：
甲：x表示 ，y表示 ；
乙：x表示 ，y表示
；
（2）求该专业户去年实际生产小麦、玉米各多少吨？（写出完整的解
答过程，
就甲或乙的思路写出一种即可）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
AE，垂足为E，
, 求
的度数。
，则
的值是 .
＝＿＿＿＿＿．