
【题目】已知,如图,点C在线段AB上,且AC=6cm,BC=14cm,点M、N分别是AC、BC的中点.
![]()
(1)求线段MN的长度;
(2)在(1)中,如果AC=acm,BC=bcm,其它条件不变,你能猜测出MN的长度吗?请说出你发现的结论,并说明理由.
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:初中数学 来源: 题型:
【题目】阅读下面材料: 在学习《圆》这一章时,老师给同学们布置了一道尺规作图题:
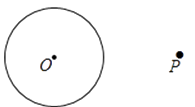
小敏的作法如下:
如图,
①链接op,做线段op的垂直平分线MN,交OP于点C
②以点C为圆心,CO的长为半径作圆,交⊙O于A、B两点
③作直线PA、PB所以直线PA,PB就是所求的切线
老师认为小敏的作法正确.
请回答:连接OA,OB后,可证∠OAP=∠OBP=90°,其依据是;由此可证明直线PA,PB都是⊙O的切线,其依据是
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,二次函数y=﹣ ![]() +bx+c的图象经过点A(1,0),且当x=0和x=5时所对应的函数值相等.一次函数y=﹣x+3与二次函数y=﹣
+bx+c的图象经过点A(1,0),且当x=0和x=5时所对应的函数值相等.一次函数y=﹣x+3与二次函数y=﹣ ![]() +bx+c的图象分别交于B,C两点,点B在第一象限.
+bx+c的图象分别交于B,C两点,点B在第一象限.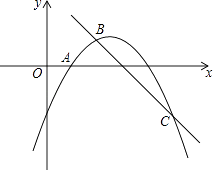
(1)求二次函数y=﹣ ![]() +bx+c的表达式;
+bx+c的表达式;
(2)连接AB,求AB的长;
(3)连接AC,M是线段AC的中点,将点B绕点M旋转180°得到点N,连接AN,CN,判断四边形ABCN的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】回答问题:
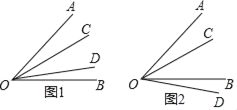
(1)已知∠AOB的度数为54°,在∠AOB的内部有一条射线OC,满足∠AOC=![]() ∠COB,在∠AOB所在平面上另有一条射线OD,满足∠BOD=
∠COB,在∠AOB所在平面上另有一条射线OD,满足∠BOD=![]() ∠AOC,如图1和图2所示,求∠COD的度数.
∠AOC,如图1和图2所示,求∠COD的度数.
(2)已知线段AB长为12cm,点C是线段AB上一点,满足AC=![]() CB,点D是直线AB上满足BD=
CB,点D是直线AB上满足BD=![]() AC.请画出示意图,求出线段CD的长.
AC.请画出示意图,求出线段CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.
(1)假设每台冰箱降价x元,商场每天销售这种冰箱的利润是y元,请写出y与x之间的函数表达式;(不要求写自变量的取值范围)
(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?
(3)每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,抛物线y=x2+bx+c与x轴只有一个交点M,与平行于x轴的直线l交于A、B两点,若AB=3,则点M到直线l的距离为( ) 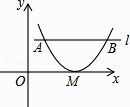
A.![]()
B.![]()
C.2
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在坐标系中放置一菱形OABC,已知∠ABC=60°,点B在y轴上,OA=1,先将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2017次,点B的落点依次为B1 , B2 , B3 , …,则B2017的坐标为( )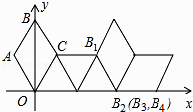
A.(1345,0)
B.(1345.5, ![]() )
)
C.(1345, ![]() )
)
D.(1345.5,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
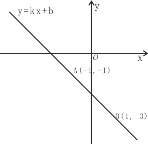
【题目】已知一次函数y=kx+b的图象经过点A(1,1)和点B(1,3).求:
(1)求一次函数的表达式;
(2)求直线AB与坐标轴围成的三角形的面积;
(3)请在x轴上找到一点P,使得PA+PB最小,并求出P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设立了可以自由转动的转盘(如图,转盘被均匀分为20份),并规定:顾客每购买200元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得200元、100元、50元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可以直接获得购物券30元.
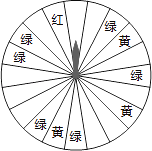
(1)求转动一次转盘获得购物券的概率;
(2)转转盘和直接获得购物券,你认为哪种方式对顾客更合算?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com