
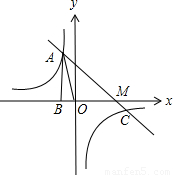
已知反比例函数![]() 图象过第二象限内的点A(-2,m)AB⊥x轴于B,Rt△AOB面积为3, 若直线y=ax+b经过点A,并且经过反比例函数
图象过第二象限内的点A(-2,m)AB⊥x轴于B,Rt△AOB面积为3, 若直线y=ax+b经过点A,并且经过反比例函数![]() 的图象上另一点C(n,—
的图象上另一点C(n,—![]() ),
),
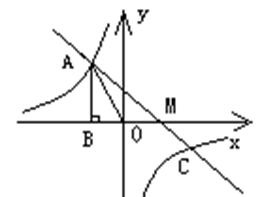
(1)求反比例函数的解析式以及直线y=ax+b的解析式;
(2)求反比例函数的值大于一次函数的值时所对应的x的取值范围。
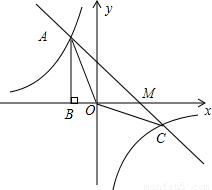
(3) 自己连接AC、和BC 并求△ABC的面积
(1)![]() ;A(-2,3);C(4,-
;A(-2,3);C(4,-![]() )….……4分
)….……4分
![]() …………6分
…………6分
(2)由图像知,交点为A(-2,3);C(4,-![]() );
);
所以当-2<x<0或x>4时,反比例函数的值大于一次函数的值。…………8分
(3)连接BC,因为![]() ,令y=0,得x=2.所以M(2,0);AB=3,
,令y=0,得x=2.所以M(2,0);AB=3,
作CD⊥x轴,则CD=![]() ; ∵A(-2,3), ∴B(-2,0),∴BM=4
; ∵A(-2,3), ∴B(-2,0),∴BM=4
![]() =
=![]() =
=![]() BM×AB+
BM×AB+ BM×CD
BM×CD
=![]() ×4×3+
×4×3+![]() ×4×
×4×![]()
=9 …………12分
解析:(1)根据Rt△AOB面积为3,A(-2,m)即可求出A点的坐标,把A点坐标代入反比例函数解析式中,求出k的值,又知反比例函数图象过C点(n,-1),代入解析式求出n的值,根据题干条件直线y=ax+b经过点A、C,已知两点坐标,列出二元一次方程组解得a和b的值,即可求出直线y=ax+b的解析式.


科目:初中数学 来源: 题型:解答题
 图象过第二象限内的点A(-2,m)AB⊥x轴于B,Rt△AOB
图象过第二象限内的点A(-2,m)AB⊥x轴于B,Rt△AOB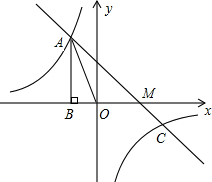 面积为3,若直线y=ax+b经过点A,并且经过反比例函数
面积为3,若直线y=ax+b经过点A,并且经过反比例函数 的图象上另一点C(n,-
的图象上另一点C(n,- ),
),查看答案和解析>>
科目:初中数学 来源:第5章《反比例函数》常考题集(13):5.2 反比例函数的图象与性质(解析版) 题型:解答题
 图象过第二象限内的点A(-2,m),AB⊥x轴于B,Rt△AOB面积为3.
图象过第二象限内的点A(-2,m),AB⊥x轴于B,Rt△AOB面积为3. )
)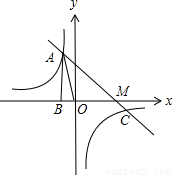
查看答案和解析>>
科目:初中数学 来源:第20章《二次函数和反比例函数》常考题集(44):20.7 反比例函数的图象、性质和应用(解析版) 题型:解答题
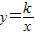 图象过第二象限内的点A(-2,m),AB⊥x轴于B,Rt△AOB面积为3,若直线y=ax+b经过点A,并且经过反比例函数
图象过第二象限内的点A(-2,m),AB⊥x轴于B,Rt△AOB面积为3,若直线y=ax+b经过点A,并且经过反比例函数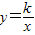 的图象上另一点C(n,-
的图象上另一点C(n,- ),
),
查看答案和解析>>
科目:初中数学 来源:第1章《反比例函数》常考题集(15):1.3 反比例函数的应用(解析版) 题型:解答题
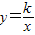 图象过第二象限内的点A(-2,m),AB⊥x轴于B,Rt△AOB面积为3.
图象过第二象限内的点A(-2,m),AB⊥x轴于B,Rt△AOB面积为3. )
)
查看答案和解析>>
科目:初中数学 来源:第23章《二次函数与反比例函数》常考题集(40):23.6 反比例函数(解析版) 题型:解答题
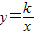 图象过第二象限内的点A(-2,m),AB⊥x轴于B,Rt△AOB面积为3.
图象过第二象限内的点A(-2,m),AB⊥x轴于B,Rt△AOB面积为3. )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com